Na czym polega nieśmiertelność? O klasyfikacji [Myślenie krytyczne #7]

kwi 29, 2022 | 2022, Myślenie krytyczne

W poprzednim artykule niniejszej serii próbowałem, Czytelniku, przekonać Cię o przydatności podziałów logicznych dla wprowadzania ładu pojęciowego. Złożoność analizowanej dziedziny sprawia jednak niekiedy, iż pojedyncze podziały, których przykłady opisywałem, są niewystarczające. W takich przypadkach przeprowadza się zwykle podziały wielostopniowe lub – jak kto woli – wielopiętrowe. Efekt wielokrotnego dzielenia zbioru obiektów należących do dziedziny jakichś rozważań nazywamy klasyfikacją tych obiektów.

Podziały wielostopniowe

Zacznijmy od przykładu. Ktoś próbuje uporządkować bogatą kolekcję własnych monet. W tym celu dzieli je na monety złote i srebrne. Jeśli w jego zbiorach nie ma monet o mieszanym składzie ani monet wykonanych z materiałów innych niż wymienione, zaproponowany podział jest zarówno rozłączny, jak i zupełny, a więc jest podziałem logicznym. Mimo to ze względów praktycznych może się on okazać niewystarczający. Na wartość monet poza rodzajem kruszcu wpływ mają przecież także inne czynniki. Kolekcjoner dzieli zatem dalej monety w każdej z wydzielonych grup według ich wagi. Za każdym razem wyróżnia monety lekkie (o masie poniżej jednej uncji), typowe (jednouncjowe) i ciężkie (o masie powyżej jednej uncji). Podziały te również są rozłączne i zupełne, a więc także są podziałami logicznymi. W ten sposób kolekcjoner podzielił swoje zbiory na sześć kategorii. Wszystkie one są między sobą rozłączne, a w sumie dają całą kolekcję. (Dla ćwiczenia spróbuj je, Czytelniku, wymienić). Na tym kolekcjoner nie musi oczywiście poprzestawać. Może dzielić swoje numizmaty dalej, przykładowo ze względu na ich pochodzenie, rok ich bicia lub z uwagi na jakiekolwiek kryterium, które wyda mu się istotne. Wynikiem tych wszystkich podziałów będzie taka lub inna klasyfikacja okazów należących do jego kolekcji.

Klasyfikacja przedmiotów należących do jakiegoś zbioru jest zatem po prostu serią podziałów. W pierwszym kroku całością dzielenia jest wyjściowy zbiór, który zostaje podzielony na ileś członów podziału. W kolejnym kroku człony pierwszego podziału traktowane są jako całości następnych podziałów. Całą procedurę można powtarzać wielokrotnie, aż do uzyskania satysfakcjonującej szczegółowości.

Wygodnym sposobem prezentowania klasyfikacji są diagramy drzewkowe. Każde piętro takiego diagramu reprezentuje kolejny podział w klasyfikacji. Poniżej znajduje się diagram przedstawiający dwa pierwsze kroki opisanej powyżej klasyfikacji monet.

Oklepanym do granic możliwości przykładem klasyfikacji jest biologiczna klasyfikacja organizmów. (Mówiąc precyzyjnie, klasyfikacji tych jest wiele, gdyż z uwagi na dokonywane odkrycia wprowadzano istotne modyfikacje. Przykładowo uważany za twórcę biologicznych klasyfikacji osiemnastowieczny szwedzki przyrodnik Karol Linneusz w pierwszym kroku dzielił wszystkie organizmy na dwa królestwa: zwierząt i roślin. Klasyfikacja prezentowana we współczesnych podręcznikach zaczyna się zwykle od wyodrębnienia trzech domen, które dopiero w kolejnym kroku dzieli się łącznie na sześć królestw.) Innymi typowymi klasyfikacjami są biblioteczne klasyfikacje książek dokonywane według coraz bardziej szczegółowych kryteriów lub podobne klasyfikacje zbiorów muzealnych. Tutaj proponuję przyjrzeć się dużo mniej znanej, a zaanonsowanej na wstępie klasyfikacji rodzajów nieśmiertelności.

Rodzaje nieśmiertelności

Istoty nieśmiertelne pojawiają się w utworach fantastycznych i fantastycznonaukowych wcale nierzadko. Co ciekawe, ich nieśmiertelność w wielu przypadkach wygląda bardzo odmiennie. Ta różnorodność nie uszła uwadze filozofów. John Martin Fischer oraz Ruth Curl zaproponowali klasyfikację pochodzących z SF modeli nieśmiertelności. (Przedstawili ją w tekście Filozoficzne modele nieśmiertelności w fantastyce naukowej, którego polskie tłumaczenie znaleźć można > tutaj. Wygląda ona mniej więcej tak.

W pierwszym kroku wszystkie przypadki nieśmiertelności podzielone zostały na te, w których nieśmiertelny jest wszechświat jako całość, oraz te, w których nieśmiertelne są istoty czujące. Ponieważ ten pierwszy rodzaj nie jest dla autorów klasyfikacji interesujący, w kolejnym kroku dzielą oni tylko przypadki tego drugiego rodzaju. Nieśmiertelność istot czujących może przyjmować formę nieatomistyczną lub atomistyczną. Z tą pierwszą mamy do czynienia wówczas, gdy poszczególne jednostki łączą się w jeden wielki byt nieśmiertelny. Z drugą, gdy jednostki wiodą własne, indywidualne niekończące się żywoty. Zarówno atomistyczne, jak i nieatomistyczne odmiany dzielą autorzy jeszcze dalej, choć każde według innego kryterium. Ponieważ wszystkie nieatomistyczne wersje okazują się ostatecznie nieatrakcyjne, uwagę skupiają na formach atomistycznych. Wśród tych zaś wyróżniają modele seryjne, wedle których jednostki przeżywają niekończącą się serię żyć, i nieseryjne, zgodnie z którymi jednostki wiodą jedno, ale niemające kresu życie. Podobnie jak na poprzednim piętrze klasyfikacji wszystkie modele seryjne, choć dające się dalej podzielić, są według autorów niepociągające. W rezultacie w ostatnim kroku skupiają się wyłącznie na odmianach nieseryjnych. (W ramach ćwiczenia spróbuj, Czytelniku, narysować diagram opisanej do tego miejsca klasyfikacji.)

Zanim przejdziemy do owego ostatniego poziomu omawianej klasyfikacji warto wskazać dwie cechy odróżniające ją od wzmiankowanej wyżej klasyfikacji monet. Po pierwsze, w przypadku tej ostatniej na każdym etapie dokonywano podziału każdego członu podziału z etapu poprzedniego (według wagi dzielono zarówno monety srebrne, jak i złote). Tak być nie musi. W klasyfikacji Fischera i Curl kategorie, które z jakichś względów uznawane są za nieciekawe, w dalszych krokach zostają pominięte, nie są dalej dzielone. Mówiąc obrazowo, nieciekawe gałęzie klasyfikacji są ucinane. Po drugie, w przypadku klasyfikacji monet wszystkie podziały jednego etapu dokonywane są z uwagi na to samo kryterium. Tak również być nie musi. Jak wspomniałem nieatomistyczne modele nieśmiertelności dzielone są według innego kryterium niż modele atomistyczne.

Podziały skrzyżowane

W ostatnim kroku klasyfikacji, a więc w przypadku nieseryjnych atomistycznych form nieśmiertelności istot czujących, Fischer i Curl przedstawiają nie jeden, ale dwa niezależne podziały. Po pierwsze, z uwagi na sposoby niekończącego się podtrzymywania życia wszystkie przypadki dzielą na te, w których wykorzystuje się jakieś metody biologiczne, i te, w których używa się metod niebiologicznych. Po drugie, ze względu na naturę życia wyróżniają modele solipsystyczne i niesolipsystyczne. (Oddzielną sprawą jest kwestia rozłączności tych podziałów.)

Choć Fischer i Curl nie piszą tego wprost, takie postawienie sprawy wydaje się sugerować, iż dwa ostatnie podziały można ze sobą skrzyżować. Najłatwiej zrozumieć, o czym tu mowa, gdy całą sprawę przedstawi się w postaci prostej tabeli.

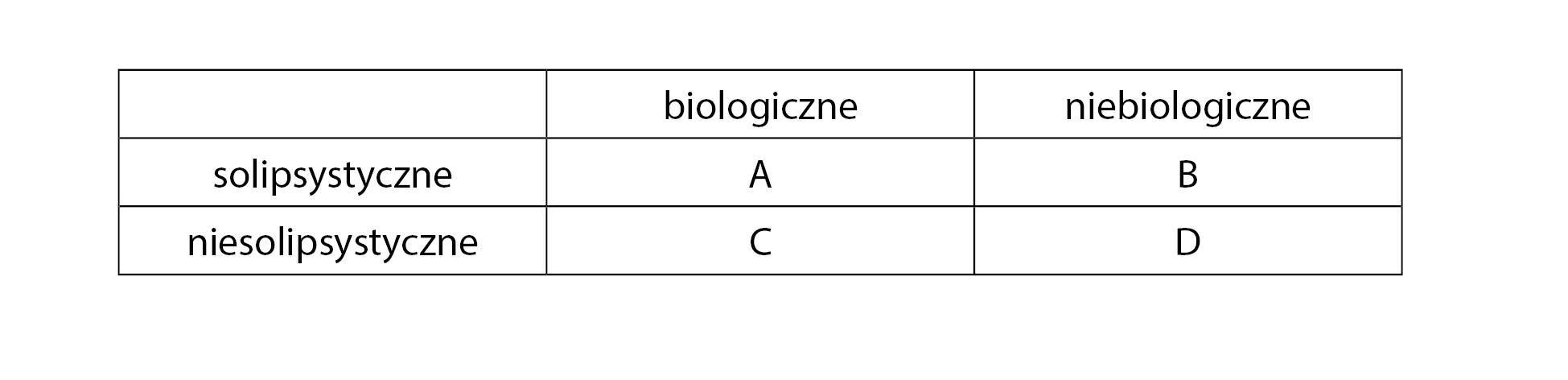Kolumny tej tabeli reprezentują człony pierwszego podziału, wiersze – człony drugiego podziału. Ponieważ oba podziały są dwuczłonowe, w rezultacie otrzymujemy cztery kategorie: A – biologiczne solipsystyczne, B – niebiologiczne solipsystyczne, C – biologiczne niesolipsystyczne oraz D – niebiologiczne niesolipsystyczne. Ten sam efekt można byłoby osiągnąć, konstruując dwustopniową klasyfikację, przy czym kolejność wykonywanych podziałów jest w ostatecznym rozrachunku nieistotna. Podobnie jest w przypadku monet. Podaną wyżej dwustopniową klasyfikację można zastąpić równoważną jej krzyżówką dwóch podziałów.

Podział rzeczowy

Na koniec chcę Cię, Czytelniku, przestrzec przed błędem, który łatwo popełnić. Może się wydawać, że podział czyjegoś życia (niekoniecznie nieśmiertelnego) na lata, tych z kolei na miesiące, a miesięcy na dni jest przykładem klasyfikacji w rozważanym obecnie sensie. Po pierwsze bowiem, każdy rok czyjegoś życia wyklucza się z wszystkimi innymi latami tegoż życia w tym sensie, że żaden z nich nie dzieje się równocześnie z innym (podobnie jest w przypadku miesięcy i dni). Po drugie, wszystkie te lata łącznie sumują się na cały ów żywot (i znowu analogicznie w przypadku miesięcy i dni).

Nie jest to jednak klasyfikacja taka, jak ją tutaj rozumiemy, ponieważ wspomniane podziały nie są podziałami logicznymi. Źródło błędu tkwi w charakterze sumowania, o którym mowa w ostatnim zdaniu poprzedniego akapitu. Podział logiczny jakiejś całości polega na wskazaniu wzajemnie rozłącznych i zupełnych członów, z których każdy jest podzbiorem dzielonej całości, podzbiorem rozumianym teoriomnogościowo. W przypadku podziału logicznego jego człony sumują się do całości w sensie teoriomnogościowym. Jest to sens, w jakim wszystkie królestwa biologiczne sumują się do zbioru wszystkich organizmów żywych. W przypadku życia dzielącego się na lata, owe lata nie są teoriomnogościowymi podzbiorami tegoż życia, ale są jego częściami. Sumują się one na całe to życie nie w sensie teoriomnogościowym, ale w takim właśnie sensie, w jakim części sumują się na całość. Takie sumowanie nazywa się sumowaniem mereologicznym i jest to zupełnie innego rodzaju operacja niż sumowanie teoriomnogościowe. Podział jakiejś całości na jej części składowe nie jest jej podziałem logicznym, ale tzw. podziałem rzeczowym.

Podział Polaków na mieszkańców poszczególnych województw, podział samochodów z uwagi na rodzaj napędu (elektryczne, benzynowe, hybrydowe itd.) lub podział organizmów żywych na przedstawicieli różnych gatunków są podziałami logicznymi. Podział Polski na województwa, podział samochodu na karoserię, silnik, zawieszenie i inne części oraz podział organizmu żywego na narządy wewnętrzne są podziałami rzeczowymi. Należy zachować czujność, aby tych dwóch rodzajów podziału nie pomylić.

Czy ludzie dzielą się na kobiety i mężczyzn? O podziale logicznym [Myślenie krytyczne #6]

kwi 22, 2022 | 2022, Myślenie krytyczne

Czy ludzie dzielą się na kobiety i mężczyzn? O podziale logicznym [Myślenie krytyczne #6]

Piotr Lipski

Według powszechnej opinii jednym z najlepszych westernów w historii kina jest wyreżyserowany przez Sergio Leone Dobry, zły i brzydki. Film przedstawia przecinające się losy trzech rewolwerowców, tytułowych: dobrego, złego i brzydkiego. Ten ostatni ma zapadający w pamięć zwyczaj dokonywania nietuzinkowych rozróżnień. Dzieli przykładowo ludzi na tych ze stryczkiem na szyi oraz tych, których rolą jest stryczek ów odciąć. Pomysł nie dziwi tak bardzo w kontekście metody zarobkowania bohatera brzydkiego. W celu wyłudzenia nagrody za własną głowę nieraz daje się on ująć przedstawicielom prawa, aby w ostatniej chwili – z pomocą dobrego – uciec spod szubienicy. W innym miejscu wszystkie ostrogi – jak nazywa rewolwerowców – klasyfikuje na tych, którzy wchodzą drzwiami, i tych, którzy wchodzą oknem. Najbardziej pamiętnego podziału dokonuje jednak w finałowej scenie nie brzydki, ale dobry. Miłośników kina podzielić można na tych, którzy ów finałowy podział uważają za mistrzowski, i tych którzy, go nie znają.

Wszystkie wspomniane podziały mają dwa niewyartykułowane wprost, choć naturalnie akceptowane założenia. Jeśli ludzie rzeczywiście dzielą się na tych ze stryczkiem i tych, co go odcinają, to znaczy, że nie ma ludzi, którzy należeliby do obu tych kategorii (mieli stryczek i go odcinali), oraz nie ma takich, którzy nie należeliby do żadnej z nich (ani nie mieli stryczka, ani go nie odcinali).

Rozłączność i zupełność

Przytoczone dwa warunki nazywamy odpowiednio warunkiem rozłączności oraz warunkiem zupełności. Charakteryzują one tzw. podziały logiczne. Przeprowadzenie podziału logicznego jakiegoś zbioru – nazywanego całością dzieloną, łac. totum divisionis – polega na podaniu kilku podzbiorów – zwanych członami podziału, łac. membra divisionis – dzielonego zbioru, w taki sposób, aby spełnione były wymienione warunki, a więc by:

(1) żaden element całości dzielonej nie należał do dwóch różnych członów podziału (warunek rozłączności);

(2) każdy element całości dzielonej należał do jakiegoś członu podziału (warunek zupełności).

Spełnienie pierwszego warunku oznacza, że człony podziału wykluczają się wzajemnie, drugiego – że sumują się do całości dzielonej. Łączne spełnienie obu warunków gwarantuje, że każdy element całości dzielonej należy do dokładnie jednego członu podziału.

Rozważmy kilka przykładów. (A) Weźmy podział ludzi (całość dzielona) na tych, którzy w danej chwili mają mniej niż 20 lat (jeden człon podziału), i tych, którzy mają więcej niż 30 lat (drugi człon podziału). Jest on podziałem rozłącznym. Nie ma bowiem człowieka, który należy zarazem do obu członów, czyli ma jednocześnie mniej niż 20 i więcej niż 30 lat. Nie jest jednak podziałem zupełnym, gdyż istnieją ludzie, którzy nie należą do żadnego członu podziału, a więc ani nie mają mniej niż 20 lat, ani nie mają więcej niż 30 lat. Ludźmi takimi są przykładowo 25-latkowie.

(B) Drugi przykład to podział ludzi (całość) na tych, którzy w danej chwili mają więcej niż 20 lat (jeden człon), i tych, którzy mają mniej niż 30 lat (drugi człon). Ponieważ istnieją ludzie, którzy mają więcej niż 20, ale mniej niż 30 lat (przykładowo wspomniani już 25-latkowie), podział ten nie spełnia warunku rozłączności. O każdym człowieku prawdą jest natomiast przynajmniej jedno z dwojga: albo ma więcej niż 20 lat, albo mniej niż 30 lat. Każdy człowiek należy zatem do jakiegoś członu podziału. Podział spełnia warunek zupełności.

Ponieważ żaden z powyższych podziałów nie spełnia zarazem obu warunków, żaden z nich nie jest podziałem logicznym. Takim podziałem jest natomiast przykładowo © podział ludzi (całość) na tych, którzy mają mniej niż 20 lat (jeden człon), i tych, którzy mają 20 lub więcej lat (drugi człon). Aby upewnić się, że rozumiesz omawiane zagadnienie, zastanów się, Czytelniku, dlaczego podział ludzi na tych, którzy mają mniej niż 20 lat i tych którzy mają więcej niż 20 lat podziałem logicznym nie jest.

Dodatkowe warunki

Powiedzmy, że ktoś proponuje, aby ludzi podzielić na tych, którzy mają mniej niż 200 lat, i tych, którzy mają więcej niż 200 lat. Być może niektórzy życzyliby sobie, aby drugi człon tego podziału nie był pusty, jednak przynajmniej na razie pozostaje on pusty. Żaden człowiek nie żył więcej niż 200 lat. W takim natomiast razie proponowany podział okazuje się bardzo osobliwy. Ostatecznie sprowadza się do podziału ludzi na tych, którzy mają mniej niż 200 lat. Mimo swojej osobliwości spełnia on zarówno warunek rozłączności, jak i zupełności. Aby zatem wyeliminować takie nieciekawe podziały, niekiedy wskazuje się dwa dodatkowe wymogi, które powinien spełnić podział logiczny.

(3) Każdy człon podziału ma być zbiorem niepustym.

(4) Muszą być wskazane przynajmniej dwa człony podziału.

Podziały dwuczłonowe i wieloczłonowe

Wszystkie rozważane powyżej podziały są podziałami dwuczłonowymi. Podział mający więcej niż dwa człony nazywa się zwykle wieloczłonowym. Takim podziałem jest przykładowo podział ludzi (całość) na mających mniej niż 20 lat (jeden człon), mających dokładnie 20 lat (drugi człon) i mających więcej niż 20 lat (trzeci człon). Zastanów się, Czytelniku, czy podział wszystkich podziałów logicznych na dwuczłonowe i wieloczłonowe jest podziałem logicznym.

Wśród podziałów dwuczłonowych wyróżnia się tzw. podziały dychotomiczne. Tworzy się je w następujący sposób. Należy wskazać jakąś cechę. Jeden człon podziału opisuje się jako zbiór przedmiotów posiadających tę cechę, drugi – jako zbiór przedmiotów nieposiadających tej cechy. Podział ludzi na 20-latków i tych, którzy nie są 20-latkami, jest przykładem takiego właśnie podziału. Inny przykład – przed przytoczeniem którego nie mogę się powstrzymać – znalazłem niedawno w odmętach Internetu. Jego autor dzieli wszystkich ludzi na tych, którzy dzielą ludzi na dwie kategorie, i tych, którzy tego nie robią.

Zasada podziału

Regułę, z uwagi na którą wyróżnia się człony podziału, nazywa się zasadą podziału (ewentualnie kryterium podziału, łac. fundamentum divisionis). Zasadą podziału większości przytoczonych powyżej przykładów był wiek. Zasadą ostatniego podziału była skłonność do tworzenia podziałów dwuczłonowych. Nie każdy podział dokonywany jest jednak z uwagi na jakąś jedną zasadę.

Przeanalizujmy przykład (D). W pewnej rodzinie jest pięcioro dzieci: 3‑, 5‑, i 6‑letni chłopcy oraz 8- i 10-letnie dziewczynki. Podzielmy wszystkie dzieci w tej rodzinie (całość) na dziewczynki (jeden człon) i dzieci mające mniej niż 7 lat (drugi człon). Podział taki jest podziałem logicznym (rozłącznym i zupełnym), mimo że jego człony nie zostały wyodrębnione z uwagi na wspólną zasadę. Pierwszy człon wyznaczono ze względu na posiadaną przez dziecko płeć, drugi – z uwagi na jego wiek.

Brak jednego kryterium nie znaczy zatem, iż dany podział nie jest podziałem logicznym. Z drugiej strony fakt, iż podział przeprowadzany jest z uwagi na jakąś jedną zasadę, nie gwarantuje, iż jest on podziałem logicznym. Człony podziałów (A) i (B) wyznaczono z uwagi na wspólną zasadę, a jednak nie są one podziałami logicznymi. Mimo to podziały według jednej zasady są w praktyce dużo częściej spotykane. W ich przypadku łatwiej bowiem o spełnienie warunków rozłączności i zupełności. Podział (D) czyni zadość obu tym wymogom, ale dzieje się tak raczej wskutek szczęśliwego zbiegu okoliczności niż w wyniku rozsądnie dobranych członów podziału.

Podziały z uwagi na jedno kryterium są ponadto bardziej naturalne. Podziały logiczne mają służyć wprowadzaniu ładu pojęciowego. Jeśli dzielimy przedmioty jakiegoś rodzaju na pewne kategorie, to zwykle chcemy, aby te wyróżnione kategorie były naturalne i aby przedmioty należące do jednej kategorii były do siebie pod istotnymi dla nas względami podobne. Najłatwiej chyba osiągnąć ten cel, wyznaczając człony podziału z uwagi na jakąś rozsądnie dobraną cechę.

Kobiety, mężczyźni i …

Uzbrojeni (po zęby) w omówione powyżej pojęcia techniczne powróćmy do wzmiankowanego na wstępie podziału ludzi na kobiety i mężczyzn. Nikogo nie trzeba chyba przekonywać, iż bywa on współcześnie kwestionowany. Teksty na ten temat publikowane były także na łamach „Filozofuj!”. Co zatem zarzuca się temu podziałowi? Aby odpowiedzieć na to pytanie spróbujmy go najpierw scharakteryzować.

Podział ten jest podziałem dwuczłonowym, choć nie jest podziałem dychotomicznym. Podziałem dychotomicznym jest podział ludzi na kobiety i nie-kobiety lub podział ludzi na mężczyzn i nie-mężczyzn. Fakt, iż jest on dwuczłonowym podziałem niedychotomicznym nie może być jednak zrzutem. Jest wiele dobrych podziałów tego typu. Ponadto łatwo wskazać naturalną zasadę tego podziału, którą jest oczywiście płeć. To także nie może być zarzutem. Wręcz przeciwnie – jest raczej zaletą. Poza tym nie ma także wątpliwości, iż podział czyni zadość warunkom (3) i (4).

Pozostaje zatem kwestia dwóch najważniejszych warunków. Uznanie tego podziału za nierozłączny równa się stwierdzeniu, iż niektórzy ludzie są jednocześnie mężczyznami i kobietami. Przy czym nie idzie tu o posiadanie pierwiastków kobiecych i męskich, ale o stuprocentowe i dosłowne bycie kobietą i mężczyzną zarazem. To „stuprocentowe i dosłowne” należy rozumieć tak, jak wtedy, gdy mówi się, iż osoba 25-letnia stuprocentowo i dosłownie jest zarówno osobą mającą mniej niż 30 lat, jak i osobą mającą więcej niż 20 lat. Sądzę, że niewielu gotowych jest przyjąć taką ewentualność.

Dużo powszechniej podważana jest zupełność rozważanego podziału. Jego krytycy zarzucają mu często „binarność”, którą należy chyba rozumieć jako dwuczłonowość. To jednak może być zarzutem tylko wtedy, gdy istnieją ludzie, którzy nie są ani mężczyznami, ani kobietami, ale raczej posiadają jakąś inną płeć albo nie posiadają jej wcale. I właśnie takiego stanowiska broni – jak sądzę – większość krytyków omawianego podziału.

Zapyta ktoś: „No dobrze, ale kto ma rację?”. Mimo iż uważam to pytanie za ważne, pozwól, Czytelniku, że w tym miejscu ucieknę przed nim. Mam ku temu dobrą wymówkę. To, czy rozważany podział jest rozłączny i zupełny nie jest kwestią logiki ani zasad krytycznego myślenia, ale kwestią badań empirycznych (biologicznych, socjologicznych i in.). Logika i zasady krytycznego myślenia wskazują, jak możemy systematycznie i poprawnie wykorzystać oraz opisać wyniki tych badań, ale ich nie przesądzają. Tylko tyle i aż tyle.

Na czym polega sepulenie? O błędnym kole w definiowaniu [Myślenie krytyczne #3]

kwi 15, 2022 | 2022, Myślenie krytyczne

Na czym polega sepulenie? O błędnym kole w definiowaniu [Myślenie krytyczne #3]

Piotr Lipski

Ijon Tichy, bohater cyklu Dzienników gwiazdowych, jest postacią, której kolejne historie Lem przedstawiał czytelnikom przez ponad trzydzieści lat. Jako jedną z pierwszych opisał wyprawę tego kosmicznego awanturnika na planetę Enteropię (Podróż czternasta). Przygotowując się do ekspedycji, Tichy postanawia poznać co nieco cel swej wędrówki. Zagląda do Encyklopedii kosmicznej, z której dowiaduje się, że Enteropię zamieszkują niejacy Ardryci. Przedstawiciele tej rasy nie tylko zmagają się ze strumami oraz polują na kurdle, ale także sepulą. Ponieważ zwłaszcza ta ostatnia czynność wydała się Tichemu tajemnicza, odszukał w Encyklopedii poświęcone jej hasło. Na niewiele się to zdało. Zanim stanie się jasne dlaczego, proponuję rozważyć kilka przykładów.

Bezpośrednie błędne koło

Weźmy takie oto zdanie:

(1) Zwierzę to zwierzę.

Jest ono w oczywisty sposób prawdziwe. Jeśli przyjmiemy, iż wyraża definicję terminu „zwierzę”, to równie oczywista staje się adekwatność tej definicji. A mimo to nikt nie uzna (1) za dobrą definicję zwierzęcia.

Proszeni o wytłumaczenie powszechnie znanych terminów odpowiadamy niekiedy w sposób podobny do (1). Każdy przeciętny użytkownik polszczyzny wie, kim są zwierzęta. Dlatego pytani o znaczenie tego słowa mówimy coś w stylu: „Zwierzę to zwierzę i koniec tematu. O czym tu więcej gadać?”. Jeśli jednak chcielibyśmy wytłumaczyć znaczenie terminu „zwierzę” komuś, kto faktycznie go nie zna, definicja (1) byłaby zupełnie nieprzydatna. Na jej podstawie nie da się odróżnić zwierzęcia od niczego innego. O czymkolwiek bowiem da się powiedzieć, iż jest ono tym, czym jest. Koń to koń, film to film, a imponderabilia to imponderabilia.

Definicja:

(2) Zwierzę to pies, kot, koń lub inne zwierzę

poprawia sytuację w niewielkim tylko stopniu. Ktoś niewiedzący uprzednio, kim są zwierzęta, dzięki (2) dowie się, iż do ich grona zaliczają się psy, koty i konie. Dalej natomiast nie będzie wiedział, co się do nich nie zalicza. Opierając się na samej tylko (2), nie sposób bowiem wykluczyć cokolwiek. Co prawda, podane przykłady można potraktować jako sugestię. Zarówno psy, koty, jak i konie żyją, zatem zapewne wśród zwierząt nie ma żadnych przedmiotów nieożywionych. Nawet jednak po uwzględnieniu tej sugestii możliwości pozostaje wiele. Wciąż nie sposób odróżnić w świetle samej tylko (2) zwierząt od przykładowo ssaków lub istot żyjących. Można się o tym przekonać, podstawiając w (2) w miejsca występowania terminu „zwierzę” odpowiednio terminy „ssak” i „istota żyjąca”. W wyniku tej czynności powstaną definicje:

(3) Ssak to pies, kot, koń lub inny ssak,

(4) Istota żyjąca to pies, kot, koń lub inna istota żyjąca.

Obie są adekwatne, ale obie tak samo jak (2) mało użyteczne.

Błąd, jaki pojawia się w definicjach (1) – (4), nazywamy bezpośrednim błędnym kołem. Polega on na tym, iż definiendum (termin definiowany) jakiejś definicji pojawia się w jej definiensie (części definiującej). W przypadku (1) mamy do czynienia ze skrajną postacią tego błędu. Definiens jest tam po prostu identyczny z definiendum. W przypadkach (2) – (4) definiendum jest tylko fragmentem definiensa, ale i tak jest to sytuacja w oczywisty sposób niepożądana. Każde bezpośrednie błędne koło jest na tyle rażące, iż błąd ten w praktyce pojawia się rzadko. Dużo częściej błędne koło przyjmuje postać bardziej zawoalowaną.

Pośrednie błędne koło

Zajrzyjmy do internetowego słownika języka polskiego PWN. Możemy tam znaleźć taką definicję:

(5) Czas to nieprzerwany ciąg chwil.

W tym samym słowniku znajdziemy też takie hasło:

(6) Chwila to krótki odcinek czasu.

Żadna z tych definicji rozważana osobno nie jest kołowata. Definiendum (5) – termin „czas” – nie pojawia się w jej definiensie. Analogicznie jest w przypadku (6). Jednak rozpatrywane łącznie definicje te zaczynają obracać się w błędnym kole.

Jeśli ktoś wie, czym jest czas, to na podstawie (6) dowie się, czym jest chwila. Jeśli rozumie, czym jest chwila, to na podstawie (5) zrozumie, czym jest czas. Jeśli natomiast nie wie ani czym jest czas, ani czym są chwile, to podane definicje nie będą dla niego zbyt pomocne. Na ich podstawie dowie się, że chwile są składnikami czasu, ale niewiele poza tym. O wielu bowiem obiektach można powiedzieć, iż są nieprzerwanymi ciągami swoich składników i opierając się na samych definicjach (5) i (6), nie sposób orzec, która z nich dotyczy czasu.

Opisaną tutaj odmianę błędnego koła nazywa się pośrednim błędnym kołem. Błąd ten pojawić się może nie w pojedynczej definicji, ale w jakimś ciągu definicji. Najprostsza jego forma jest następująca. Jakiś termin A definiuje się przy użyciu jakiegoś innego terminu B, a następnie ten inny termin B definiuje się przy pomocy A. Definicje (5) i (6) są tego szczególnym przypadkiem (czas definiuje się przez odwołanie do chwili, a chwilę – odwołując się do czasu). W ogólności ciąg definicji, o którym tu mowa, może być dłuższy, ale w przypadku jakiegokolwiek pośredniego błędnego koła definiendum każdej kolejnej definicji w ciągu pojawia się w definiensie poprzedniej, a ponadto w definiensie ostatniej pojawia się definiendum pierwszej (co zamyka koło).

Czy można uniknąć błędnego koła?

Wskazane powyżej pośrednie błędne koło nie jest jedynym obecnym w słowniku PWN (spróbuj się o tym przekonać, Czytelniku, samodzielnie). Podobnie zresztą wygląda sytuacja w przypadku jakiegokolwiek innego wystarczająco obszernego słownika. Jeśli się chwilę nad tym zastanowić, nie wydaje się to nawet zaskakujące. W porządnym słowniku jakiegoś języka powinny pojawić się definicje wszystkich słów tego języka. Jednocześnie wszystkie te definicje spisane są właśnie w tym języku. W takim razie, chociaż można (i należy) unikać bezpośrednich kół, jakieś pośrednie koła na pewno się pojawią. Dlatego też nie sposób nauczyć się języka, korzystając wyłącznie z jego słownika. Jakiś podstawowy zasób słownictwa trzeba przyswoić sobie inaczej, np. obcując z użytkownikami języka. Tą uwagą wpływam jednak na bardzo niepewne wody, a zatem zawracam.

Na marginesie dodam, iż całkowita eliminacja kołowatości w definiowaniu możliwa jest chyba tylko w przypadku formalnych systemów aksjomatycznych. Odbywa się ona kosztem przyjęcia pewnych terminów, nazywanych terminami pierwotnymi danego systemu, bez definicji. Wprowadzenie terminu pierwotnego do teorii polega na jego użyciu w aksjomatach (założeniach, które przyjmuje się bez dowodu) tej teorii. Języki naturalne tak nie działają.

Sepulenie

W słownikach języków naturalnych kołowatości nie da się zupełnie wyeliminować, ale należy minimalizować ich niepożądane skutki. Wszystkie podane dotychczas definicje były w taki czy inny sposób kołowate. Może Ci się to jednak, Czytelniku, wydawać mało problematyczne. Jeśli tak jest, to zapewne dlatego, że definiowane terminy dobrze rozumiesz. Aby przekonać się, że kołowatość w definiowaniu może być rzeczywiście kłopotliwa, wróćmy do definicji, jakie w Encyklopedii kosmicznej znalazł Ijon Tichy.

Brzmiały one mniej więcej tak (dla uproszczenia pozwoliłem sobie na drobne zmiany w tekście Lema, które – jak sądzę – są jednak zgodne z duchem oryginału):

(7) SEPULENIE – czynność Ardrytów z planety Enteropii, wykonywana przy pomocy sepulkariów,

(8) SEPULKARIA – obiekty służące do sepulenia.

Zarówno Tichy, jak i my dowiadujemy się czegoś z powyższych określeń. Wiemy przykładowo, że sepulenie jest czynnością, która wymaga pewnych specjalnych przedmiotów do jej wykonania. Tego, na czym konkretnie polega ta czynność, nie sposób już zgadnąć. O ile dla nas ignorancja ta jest niegroźna, o tyle biednemu Ijonowi przysporzyła niejakich przykrości w czasie jego pobytu na Enteropii. I mimo iż dowiedział się jeszcze paru rzeczy o sepuleniu, to zarówno dla niego, jak i dla nas prawdziwa natura tej czynności pozostaje tajemnicą.

Idem per idem a ignotum per ignotum

Jedno z łacińskich określeń na błędne koło brzmi: idem per idem, co w dosłownym tłumaczeniu oznacza: to samo przez to samo. Nie należy go mylić z innym określeniem, a mianowicie ignotum per ignotum, oznaczającym z kolei: nieznane przez nieznane. Błąd ignotum per ignotum popełnia ktoś, kto definiuje (lub tłumaczy) jakiś niezrozumiały termin, używając terminów równie, a może nawet bardziej niezrozumiałych. Przykładowo definicja (7) zawiera taki właśnie błąd, gdyż ktoś nieznający terminu „sepulenie” zapewne nie będzie znał także terminu „sepulkarium”.

Jedna z głównych różnic pomiędzy idem per idem a ignotum per ignotum polega na tym, że ten pierwszy błąd zależy wyłącznie od struktury definicji, a ten drugi od zamierzonego odbiorcy definicji. O ile definicja albo po prostu jest, albo nie jest kołowata (idem per idem), o tyle ta sama definicja może być niezrozumiała (ignotum per ignotum) dla jednego odbiorcy, a dla drugiego już taka nie być. Definicja (7) dla Tichego jest niezrozumiała, ale dla przeciętnego Ardryty zapewne taka nie jest.

Z całą pewnością wiele definicji kołowatych jest też niezrozumiałych. Czy jest tak zawsze? Nad tym, Czytelniku, zastanów się samodzielnie.

Piotr Lipski: #3. Na czym polega sepulenie? O błędnym kole w definiowaniu [Myślenie krytyczne]

Czy szympans jest osobą? O precyzji terminologicznej [Myślenie krytyczne #2]

kwi 12, 2022 | 2022, Myślenie krytyczne

Kilka lat temu amerykańska organizacja Nonhuman Rights Project (NhRP) próbowała wywalczyć wolność dla Kiko i Tommy’ego, dwóch szympansów trzymanych w niewoli. Przedstawiciele NhRP starali się przekonać sąd w Nowym Yorku, że szympansy są osobami, a w związku z tym przysługują im prawa, w szczególności prawo do wolności. Choć ostatecznie sąd nie zgodził się z argumentacją obrońców zwierząt, to jednak potraktował sprawę poważnie i dostrzegł jej złożoność. Spór wokół podmiotowości Kiko i Tommy’ego był sporem o definicję osoby. Aby móc go właściwie zanalizować, należy dobrze rozumieć, na czym polega adekwatność definicji.

Definicje adekwatne

Nazw używamy zwykle, aby przy ich pomocy odnosić się do pewnych obiektów w świecie, aby w jakiś sposób wskazywać te obiekty, głównie po to, żeby – w dalszej perspektywie – móc coś o nich stwierdzać. Obiekty, do których odnosimy się przy użyciu pewnej nazwy, zwiemy desygnatami tej nazwy. Desygnatem nazwy „kontynent” jest zatem przykładowo Europa lub Afryka, a desygnatem nazwy „największy kontynent na Ziemi” jest Azja. Zbiór (w sensie dystrybutywnym, czyli składający się z elementów, nie z części) wszystkich desygnatów jakiejś nazwy jest jej zakresem. Zatem zakresem nazwy „kontynent” jest zbiór wszystkich kontynentów, natomiast zakresem nazwy „największy kontynent na Ziemi” jest zbiór jednoelementowy, którego jedyny element to Azja (taki zbiór jest czymś innym niż Azja!).

Definicja adekwatna to taka, w przypadku której zakres terminu definiowanego (definiendum) jest identyczny z zakresem członu definiującego (definiens), czyli każdy desygnat definiendum jest desygnatem definiensa i odwrotnie. Rozważmy definicję:

(B) Babcia jakiejś osoby to matka rodzica tej osoby.

Definicja ta jest adekwatna, ponieważ każda babcia pewnej osoby jest matką rodzica tej osoby oraz jednocześnie każda matka rodzica tej osoby jest jej babcią. Warto dodać, że taki zestaw cech, jak ten wskazany w definicji (B), a więc zestaw cech przysługujących wszystkim desygnatom danej nazwy i tylko im, nazywamy jej treścią charakterystyczną. Treścią charakterystyczną nazwy „babcia jakiejś osoby” jest cecha polegająca na byciu „matką rodzica tej osoby”.

Rodzaje nieadekwatności

Definicja może być nieadekwatna na cztery sposoby. Po pierwsze, może być za szeroka. Dzieje się tak, jeżeli zakres definiendum jest podzbiorem właściwym zakresu definiensa. Przyjrzyjmy się definicji:

(1) Babcia jakiejś osoby to rodzic rodzica tej osoby.

Jest ona za szeroka, ponieważ każda babcia jest rodzicem rodzica, ale nie odwrotnie. Są przecież jeszcze dziadkowie.

Może się zdarzyć sytuacja odwrotna, a więc definicja, w przypadku której to zakres definiensa jest podzbiorem właściwym zakresu definiendum. Taką definicję nazywamy za wąską, a oto jej przykład:

(2) Babcia jakiejś osoby to matka matki tej osoby.

Rzeczywiście każda matka matki jest babcią, ale są babcie (te ze strony ojca) niespełniające tego warunku.

W pierwszej chwili może się to wydawać nieintuicyjne, ale są także definicje za szerokie i za wąskie jednocześnie (tyle, że w różnych odniesieniach), jak przykładowo:

(3) Babcia jakiejś osoby to rodzic matki tej osoby.

W takim przypadku zakresy definiendum oraz definiensa krzyżują się. Znaczy to, że są obiekty należące do obu tych zakresów  a), ale są też obiekty należące do pierwszego z nich, a nienależące do drugiego b) oraz odwrotnie c). W tym konkretnym przypadku są: a) babcie będące rodzicem matki (babcie ze strony matki; wspólne desygnaty definiendum i definiensa), b) babcie niebędące rodzicem matki (babcie ze strony ojca; desygnaty definiendum, ale nie definiensa) oraz c) rodzice matki niebędący babciami (dziadkowie ze strony matki; desygnaty definiensa, ale nie definiendum).

Skrajnie nieadekwatnymi definicjami są te, w których zakresy definiendum i definiensa zupełnie się wykluczają, a więc nie mają żadnych elementów wspólnych. Najczęstszym chyba przypadkiem takiej nieadekwatności są definicje zawierające błąd przesunięcia kategorialnego, o którym pisałem poprzednim razem, a który pojawia się przykładowo w takiej oto definicji:

(4) Babcia to najbliższa rodzina.

Babcia nie jest rodziną, ponieważ babcia to zawsze konkretna osoba, a rodzina to z kolei jakaś grupa osób.

Terminy niewyraźne i nieostre

Termin „babcia”, mimo iż należy do języka potocznego, jest całkiem precyzyjny. W jego przypadku dość łatwo podać definicję adekwatną, a także wskazać ewentualne nieadekwatności w definicji. Wiele wyrażeń używanych w codziennych, zwykłych rozmowach nie jest jednak tak ściśle określonych. Aby się o tym przekonać wystarczy otworzyć słownik.

Weźmy przykładowo następującą definicję z internetowego słownika języka polskiego PWN:

(K) Krzesło to mebel służący do siedzenia, mający z tyłu oparcie.

Jest to oczywiście definicja za szeroka. Pod definiens podpadają przykładowo sofy, które krzesłami nie są. Co gorsza jednak, nie bardzo wiadomo, jak należałoby przeformułować powyższą definicję, aby była ona adekwatna. Możesz się, Czytelniku, pokusić o znalezienie takiego przeformułowania, ale ostrzegam, że nie jest to zadanie proste, jeśli w ogóle wykonalne. Wyrażenia takie jak „krzesło”, w przypadku których trudne lub wręcz niemożliwe jest wskazanie treści charakterystycznej, nazywamy terminami niewyraźnymi.

Nazwa „krzesło”, mimo iż niewyraźna, jest jednak ostra. Nie jest łatwo wskazać cechy, które przysługują wszystkim krzesłom i tylko im, jednak w każdym konkretnym przypadku (przynajmniej z rozsądnym przybliżeniem) jesteśmy w stanie bez większych trudności zdecydować, czy dany przedmiot jest krzesłem, czy też nie. Są jednak terminy, które nie posiadają tej cechy. Wzorcowym przykładem takiej nazwy nieostrej jest wyraz „łysy”. Chociaż w przypadku niektórych osób nie mamy wątpliwości, iż są łyse, a w przypadku innych jesteśmy pewni, iż łyse nie są, to jednak znajdą się i tacy, którzy cechują się wysokim już czołem, ale wciąż mają jeszcze co zaczesać. Tych ostatnich trudno będzie nam jednoznacznie zaklasyfikować.

Zarówno nieostrość, jak i niewyraźność traktowane są często jako wady (spróbuj, Czytelniku, określić łączące je zależności). W przypadku języka potocznego nie są to wady zbyt poważne. O ile rozmówcy są ich świadomi, nie przeszkadzają one w zwykłym komunikowaniu się. Bardziej zgubne byłyby raczej uporczywe próby usuwania tych niedoskonałości. Przesadna precyzja w mowie potocznej jest zwykle komiczna albo uciążliwa. Istnieją jednak dziedziny, w których nieostra i niewyraźna terminologia jest szczególnie niepożądana. Poza naukowcami bardzo uważni w tym względzie powinni być prawnicy.

Kim jest osoba?

Jeśli ufać słownikom, to potoczne znaczenie terminu „osoba” jest zaskakująco precyzyjne. Wspomniany już słownik PWN podaje, że jest to „jednostka ludzka”, natomiast według brytyjskiego Cambridge i amerykańskiego Merriam-Webster jest to „istota ludzka” (a human being). Rzeczywiście w mowie potocznej nazwy „osoba” często używamy zamiennie z nazwą „człowiek”. Jest jednak sporo powodów, dla których wielu myślicieli uważa taką definicję za nieadekwatną. Niniejszy artykuł nie jest miejscem na ich nawet pobieżny przegląd (zainteresowanego Czytelnika odsyłam do numeru 22/2018 „Filozofuj!”, w całości poświęconego temu zagadnieniu). Warto jednak przytoczyć tutaj uwagi poczynione przez jednego z obrońców wspomnianych na wstępie szympansów.

Jeff Sebo, filozof z New York University, w artykule opisującym całą sprawę zauważa, że kategorię osoby przyznajemy pewnym istotom nie dlatego, że są przedstawicielami takiego a nie innego gatunku biologicznego, ale raczej dlatego, że charakteryzują się pewnymi zdolnościami. Definicje tego typu bywają jednak węższe (eksluzywne) lub szersze (inkluzywne). Do tych pierwszych zalicza się przykładowo propozycja, aby za osobę uważać jednostkę zdolną do używania języka i przeprowadzania abstrakcyjnych rozumowań. Przy takim postawieniu sprawy żadnego, albo niemal żadnego, zwierzęcia nie obejmie zakres nazwy „osoba”. Jednak nie znajdą się w nim również niektórzy ludzie (np. małe dzieci). Proponowane są zatem definicje wyznaczające szerszy zakres omawianej nazwy, uznające za osoby istoty zdolne do odczuwania emocji (przynajmniej niektórych), własnej tożsamości (chociaż w jakimś podstawowym stopniu) oraz przywiązania do innych. Konsekwencją przyjęcia takiej definicji jest przyznanie statusu osoby nie tylko ludziom (choć być może nie wszystkim), ale także wielu zwierzętom.

Nowojorski sąd rozstrzygający sprawę Kiko i Tommy’ego opowiedział się za jednym z rozwiązań ekskluzywnych. Sąd argentyński w podobnej sprawie przyjął opcję inkluzywną i w 2016 roku nadał osobowy status szympansicy o imieniu Cecilia. W Nowej Zelandii i w Indiach przyjęto jeszcze dalej idące rozwiązania, uznając za osoby pewne rzeki. Wszystko to pokazuje, iż mimo wielowiekowych debat termin „osoba” wciąż pozostaje nieprecyzyjny. To, jak będzie on uściślany w różnych systemach prawnych, jest zagadnieniem nie tylko teoretycznym, ale mającym także dalekosiężne skutki praktyczne.