W poprzednim artykule niniejszej serii próbowałem, Czytelniku, przekonać Cię o przydatności podziałów logicznych dla wprowadzania ładu pojęciowego. Złożoność analizowanej dziedziny sprawia jednak niekiedy, iż pojedyncze podziały, których przykłady opisywałem, są niewystarczające. W takich przypadkach przeprowadza się zwykle podziały wielostopniowe lub – jak kto woli – wielopiętrowe. Efekt wielokrotnego dzielenia zbioru obiektów należących do dziedziny jakichś rozważań nazywamy klasyfikacją tych obiektów.
Podziały wielostopniowe
Zacznijmy od przykładu. Ktoś próbuje uporządkować bogatą kolekcję własnych monet. W tym celu dzieli je na monety złote i srebrne. Jeśli w jego zbiorach nie ma monet o mieszanym składzie ani monet wykonanych z materiałów innych niż wymienione, zaproponowany podział jest zarówno rozłączny, jak i zupełny, a więc jest podziałem logicznym. Mimo to ze względów praktycznych może się on okazać niewystarczający. Na wartość monet poza rodzajem kruszcu wpływ mają przecież także inne czynniki. Kolekcjoner dzieli zatem dalej monety w każdej z wydzielonych grup według ich wagi. Za każdym razem wyróżnia monety lekkie (o masie poniżej jednej uncji), typowe (jednouncjowe) i ciężkie (o masie powyżej jednej uncji). Podziały te również są rozłączne i zupełne, a więc także są podziałami logicznymi. W ten sposób kolekcjoner podzielił swoje zbiory na sześć kategorii. Wszystkie one są między sobą rozłączne, a w sumie dają całą kolekcję. (Dla ćwiczenia spróbuj je, Czytelniku, wymienić). Na tym kolekcjoner nie musi oczywiście poprzestawać. Może dzielić swoje numizmaty dalej, przykładowo ze względu na ich pochodzenie, rok ich bicia lub z uwagi na jakiekolwiek kryterium, które wyda mu się istotne. Wynikiem tych wszystkich podziałów będzie taka lub inna klasyfikacja okazów należących do jego kolekcji.
Klasyfikacja przedmiotów należących do jakiegoś zbioru jest zatem po prostu serią podziałów. W pierwszym kroku całością dzielenia jest wyjściowy zbiór, który zostaje podzielony na ileś członów podziału. W kolejnym kroku człony pierwszego podziału traktowane są jako całości następnych podziałów. Całą procedurę można powtarzać wielokrotnie, aż do uzyskania satysfakcjonującej szczegółowości.
Wygodnym sposobem prezentowania klasyfikacji są diagramy drzewkowe. Każde piętro takiego diagramu reprezentuje kolejny podział w klasyfikacji. Poniżej znajduje się diagram przedstawiający dwa pierwsze kroki opisanej powyżej klasyfikacji monet.

Oklepanym do granic możliwości przykładem klasyfikacji jest biologiczna klasyfikacja organizmów. (Mówiąc precyzyjnie, klasyfikacji tych jest wiele, gdyż z uwagi na dokonywane odkrycia wprowadzano istotne modyfikacje. Przykładowo uważany za twórcę biologicznych klasyfikacji osiemnastowieczny szwedzki przyrodnik Karol Linneusz w pierwszym kroku dzielił wszystkie organizmy na dwa królestwa: zwierząt i roślin. Klasyfikacja prezentowana we współczesnych podręcznikach zaczyna się zwykle od wyodrębnienia trzech domen, które dopiero w kolejnym kroku dzieli się łącznie na sześć królestw.) Innymi typowymi klasyfikacjami są biblioteczne klasyfikacje książek dokonywane według coraz bardziej szczegółowych kryteriów lub podobne klasyfikacje zbiorów muzealnych. Tutaj proponuję przyjrzeć się dużo mniej znanej, a zaanonsowanej na wstępie klasyfikacji rodzajów nieśmiertelności.
Rodzaje nieśmiertelności
Istoty nieśmiertelne pojawiają się w utworach fantastycznych i fantastycznonaukowych wcale nierzadko. Co ciekawe, ich nieśmiertelność w wielu przypadkach wygląda bardzo odmiennie. Ta różnorodność nie uszła uwadze filozofów. John Martin Fischer oraz Ruth Curl zaproponowali klasyfikację pochodzących z SF modeli nieśmiertelności. (Przedstawili ją w tekście Filozoficzne modele nieśmiertelności w fantastyce naukowej, którego polskie tłumaczenie znaleźć można > tutaj. Wygląda ona mniej więcej tak.
W pierwszym kroku wszystkie przypadki nieśmiertelności podzielone zostały na te, w których nieśmiertelny jest wszechświat jako całość, oraz te, w których nieśmiertelne są istoty czujące. Ponieważ ten pierwszy rodzaj nie jest dla autorów klasyfikacji interesujący, w kolejnym kroku dzielą oni tylko przypadki tego drugiego rodzaju. Nieśmiertelność istot czujących może przyjmować formę nieatomistyczną lub atomistyczną. Z tą pierwszą mamy do czynienia wówczas, gdy poszczególne jednostki łączą się w jeden wielki byt nieśmiertelny. Z drugą, gdy jednostki wiodą własne, indywidualne niekończące się żywoty. Zarówno atomistyczne, jak i nieatomistyczne odmiany dzielą autorzy jeszcze dalej, choć każde według innego kryterium. Ponieważ wszystkie nieatomistyczne wersje okazują się ostatecznie nieatrakcyjne, uwagę skupiają na formach atomistycznych. Wśród tych zaś wyróżniają modele seryjne, wedle których jednostki przeżywają niekończącą się serię żyć, i nieseryjne, zgodnie z którymi jednostki wiodą jedno, ale niemające kresu życie. Podobnie jak na poprzednim piętrze klasyfikacji wszystkie modele seryjne, choć dające się dalej podzielić, są według autorów niepociągające. W rezultacie w ostatnim kroku skupiają się wyłącznie na odmianach nieseryjnych. (W ramach ćwiczenia spróbuj, Czytelniku, narysować diagram opisanej do tego miejsca klasyfikacji.)
Zanim przejdziemy do owego ostatniego poziomu omawianej klasyfikacji warto wskazać dwie cechy odróżniające ją od wzmiankowanej wyżej klasyfikacji monet. Po pierwsze, w przypadku tej ostatniej na każdym etapie dokonywano podziału każdego członu podziału z etapu poprzedniego (według wagi dzielono zarówno monety srebrne, jak i złote). Tak być nie musi. W klasyfikacji Fischera i Curl kategorie, które z jakichś względów uznawane są za nieciekawe, w dalszych krokach zostają pominięte, nie są dalej dzielone. Mówiąc obrazowo, nieciekawe gałęzie klasyfikacji są ucinane. Po drugie, w przypadku klasyfikacji monet wszystkie podziały jednego etapu dokonywane są z uwagi na to samo kryterium. Tak również być nie musi. Jak wspomniałem nieatomistyczne modele nieśmiertelności dzielone są według innego kryterium niż modele atomistyczne.
Podziały skrzyżowane
W ostatnim kroku klasyfikacji, a więc w przypadku nieseryjnych atomistycznych form nieśmiertelności istot czujących, Fischer i Curl przedstawiają nie jeden, ale dwa niezależne podziały. Po pierwsze, z uwagi na sposoby niekończącego się podtrzymywania życia wszystkie przypadki dzielą na te, w których wykorzystuje się jakieś metody biologiczne, i te, w których używa się metod niebiologicznych. Po drugie, ze względu na naturę życia wyróżniają modele solipsystyczne i niesolipsystyczne. (Oddzielną sprawą jest kwestia rozłączności tych podziałów.)
Choć Fischer i Curl nie piszą tego wprost, takie postawienie sprawy wydaje się sugerować, iż dwa ostatnie podziały można ze sobą skrzyżować. Najłatwiej zrozumieć, o czym tu mowa, gdy całą sprawę przedstawi się w postaci prostej tabeli.
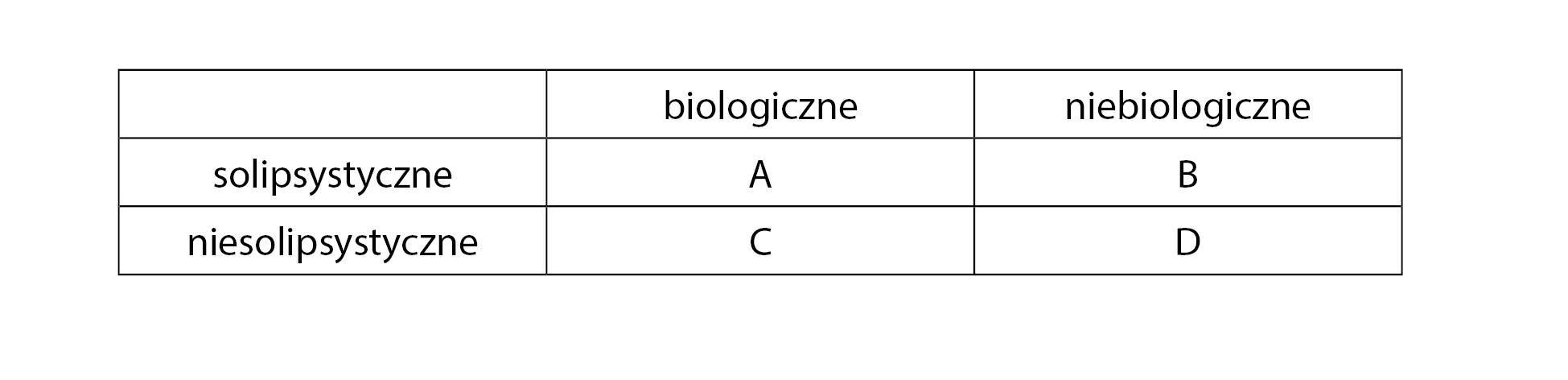 Kolumny tej tabeli reprezentują człony pierwszego podziału, wiersze – człony drugiego podziału. Ponieważ oba podziały są dwuczłonowe, w rezultacie otrzymujemy cztery kategorie: A – biologiczne solipsystyczne, B – niebiologiczne solipsystyczne, C – biologiczne niesolipsystyczne oraz D – niebiologiczne niesolipsystyczne. Ten sam efekt można byłoby osiągnąć, konstruując dwustopniową klasyfikację, przy czym kolejność wykonywanych podziałów jest w ostatecznym rozrachunku nieistotna. Podobnie jest w przypadku monet. Podaną wyżej dwustopniową klasyfikację można zastąpić równoważną jej krzyżówką dwóch podziałów.
Kolumny tej tabeli reprezentują człony pierwszego podziału, wiersze – człony drugiego podziału. Ponieważ oba podziały są dwuczłonowe, w rezultacie otrzymujemy cztery kategorie: A – biologiczne solipsystyczne, B – niebiologiczne solipsystyczne, C – biologiczne niesolipsystyczne oraz D – niebiologiczne niesolipsystyczne. Ten sam efekt można byłoby osiągnąć, konstruując dwustopniową klasyfikację, przy czym kolejność wykonywanych podziałów jest w ostatecznym rozrachunku nieistotna. Podobnie jest w przypadku monet. Podaną wyżej dwustopniową klasyfikację można zastąpić równoważną jej krzyżówką dwóch podziałów.
Podział rzeczowy
Na koniec chcę Cię, Czytelniku, przestrzec przed błędem, który łatwo popełnić. Może się wydawać, że podział czyjegoś życia (niekoniecznie nieśmiertelnego) na lata, tych z kolei na miesiące, a miesięcy na dni jest przykładem klasyfikacji w rozważanym obecnie sensie. Po pierwsze bowiem, każdy rok czyjegoś życia wyklucza się z wszystkimi innymi latami tegoż życia w tym sensie, że żaden z nich nie dzieje się równocześnie z innym (podobnie jest w przypadku miesięcy i dni). Po drugie, wszystkie te lata łącznie sumują się na cały ów żywot (i znowu analogicznie w przypadku miesięcy i dni).
Nie jest to jednak klasyfikacja taka, jak ją tutaj rozumiemy, ponieważ wspomniane podziały nie są podziałami logicznymi. Źródło błędu tkwi w charakterze sumowania, o którym mowa w ostatnim zdaniu poprzedniego akapitu. Podział logiczny jakiejś całości polega na wskazaniu wzajemnie rozłącznych i zupełnych członów, z których każdy jest podzbiorem dzielonej całości, podzbiorem rozumianym teoriomnogościowo. W przypadku podziału logicznego jego człony sumują się do całości w sensie teoriomnogościowym. Jest to sens, w jakim wszystkie królestwa biologiczne sumują się do zbioru wszystkich organizmów żywych. W przypadku życia dzielącego się na lata, owe lata nie są teoriomnogościowymi podzbiorami tegoż życia, ale są jego częściami. Sumują się one na całe to życie nie w sensie teoriomnogościowym, ale w takim właśnie sensie, w jakim części sumują się na całość. Takie sumowanie nazywa się sumowaniem mereologicznym i jest to zupełnie innego rodzaju operacja niż sumowanie teoriomnogościowe. Podział jakiejś całości na jej części składowe nie jest jej podziałem logicznym, ale tzw. podziałem rzeczowym.
Podział Polaków na mieszkańców poszczególnych województw, podział samochodów z uwagi na rodzaj napędu (elektryczne, benzynowe, hybrydowe itd.) lub podział organizmów żywych na przedstawicieli różnych gatunków są podziałami logicznymi. Podział Polski na województwa, podział samochodu na karoserię, silnik, zawieszenie i inne części oraz podział organizmu żywego na narządy wewnętrzne są podziałami rzeczowymi. Należy zachować czujność, aby tych dwóch rodzajów podziału nie pomylić.