mar 29, 2025 | 2025, aktualności
Zasady rozwiązywania testu i punktacja:
- Jest to test wielokrotnego wyboru. W każdym pytaniu wykluczona jest tylko taka możliwość, że żadna odpowiedź nie jest poprawna.
- Za każde pytanie można otrzymać 0 pkt. lub 1 pkt.
- Za brak odpowiedzi lub odpowiedź błędną otrzymuje się 0 pkt.
- Za odpowiedź poprawną zostaje przyznany 1 pkt. niezależnie od tego, ile właściwych opcji odpowiedzi jest w danym pytaniu (może być jedna prawdziwa albo dwie prawdziwe, albo trzy prawdziwe, albo cztery). Punkt zostanie przyznany tylko wówczas, gdy zaznaczone są wszystkie i wyłącznie prawdziwe opcje, czyli gdy nie jest zaznaczona żadna błędna odpowiedź.
Przypominamy, że to jest test próbny. Ten test możecie rozwiązywać wiele razy. W tym teście nie ma ustawionego limitu czasu.
W teście zastosowano sekwencyjną metodę nawigacji.
Życzymy Wam powodzenia!
Materiały przygotowujace do etapu szkolnego
NET FOR LOGIC
mar 28, 2025 | 2025, aktualności
Etap Szkolny XIII Ogólnopolskiego Konkursu Logicznego zostanie przeprowadzony online na platformie Moodle. Dlatego każdy uczeń – uczestnik I etapu Konkursu NIEZALEŻNIE OD REJESTRACJI UCZESTNICTWA na stronie https://konkurslogiczny.kul.pl/rejestracja/ powinien samodzielnie założyć dla siebie konto w serwisie logika.kul.pl [https://logika.kul.pl/]. Jeśli uczestnik brał udział w poprzednich edycjach konkursu może skorzystać z dotychczasowego konta.
Podczas rejestracji konta na Twój adres email zostanie wysłany link potwierdzający. Po kliknięciu w link zostaniesz przekierowany ponownie do serwisu Moodle i poproszony/-a o uzupełnienie danych Twojego profilu (uczestnicy podają dane adresowe szkoły włącznie z numerem REGON [Jak uzupełnić dane uczestnika Konkursu?]). Te dane możesz nawet uzupełnić później, tj. po samodzielnym zapisaniu się na kurs 'XIII Ogólnopolski Konkurs Logiczny’.
Jak samodzielnie zapisać się na kurs 'XIII Ogólnopolski Konkurs Logiczny’
Jeśli zmodyfikujesz swój profil i zapiszesz zmiany, kliknij w zakładkę Strona główna, a następnie w pole „Dostępne kursy”. Po wybraniu pola 'XIII Ogólnopolski Konkurs Logiczny’ z pewnością zauważysz klawisz umożliwiający samodzielne zapisanie się na ten kurs. Tylko osoby zapisane na kurs ’XIII Ogólnopolski Konkurs Logiczny’ będą mogły przystąpić do testu próbnego i testu Etapu Szkolnego Konkursu.
W tej chwili w kursie XIII OKL dostępne są test próbny i informacje o Net for Logic – cyklu webinarów e-learningowych. Warto posłuchać tych wykładów, ponieważ zaprezentowane w nich materiały mogą zostać wykorzystane w Etapie Szkolnym Konkursu.
Jeśli masz jakiejkolwiek trudności z rejestracją napisz do nas na adres logika @ kul.pl.
Serdecznie Cię pozdrawiamy
Organizatorzy konkursu Logicznego
Jak uzupełnić dane uczestnika Konkursu?
XIII Ogólnopolski Konkurs Logiczny – TEST PRÓBNY
mar 28, 2025 | 2025, aktualności
Uczestniku Konkursu,
jeśli założyłe(-a)ś konto w serwisie logika.kul.pl, bardzo prosimy, uzupełnij Twoje dane o szkole, w której się uczysz.
Aktualizacja Twoich danych ma dla nas priorytetowe znaczenie, ponieważ dzięki temu w szkole, w której się uczysz i napiszesz test etapu szkolnego będziemy mogli potwierdzić Twoją tożsamość.
Jak to zrobić?
Zaloguj się do serwisu Ogólnopolskiego Konkursu Logicznego na stronie https://logika.kul.pl, a następnie postępuj zgodnie z poniższą instrukcją.
W prawym górnym rogu kliknij na konto użytkownika i rozwiń listę. Wybierz „Profil”, a następnie „Modyfikuj profil”.
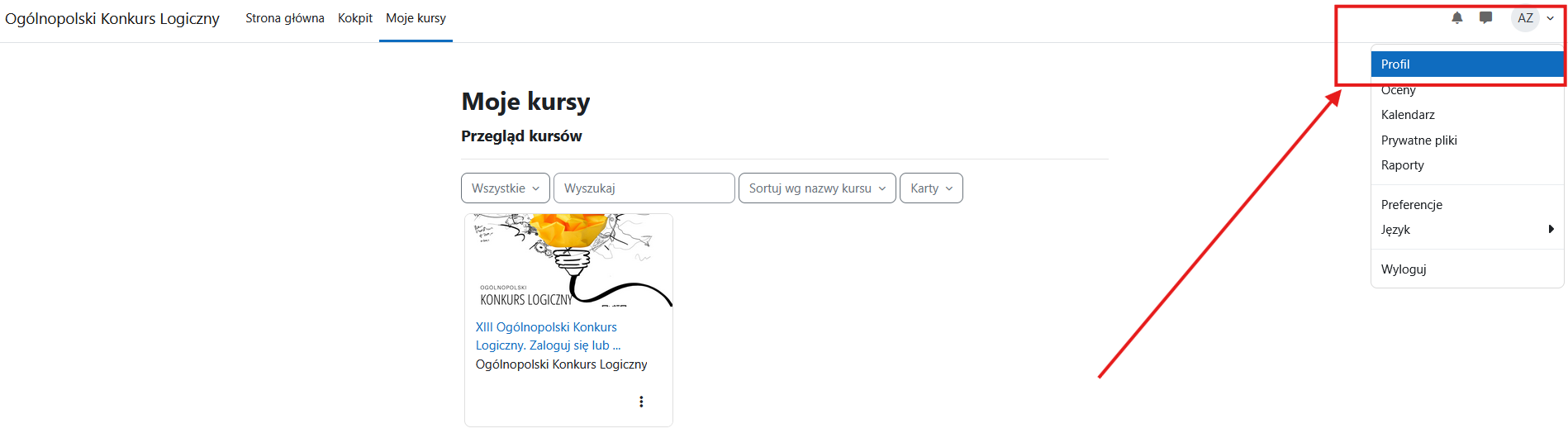
Przewiń listę do dołu.
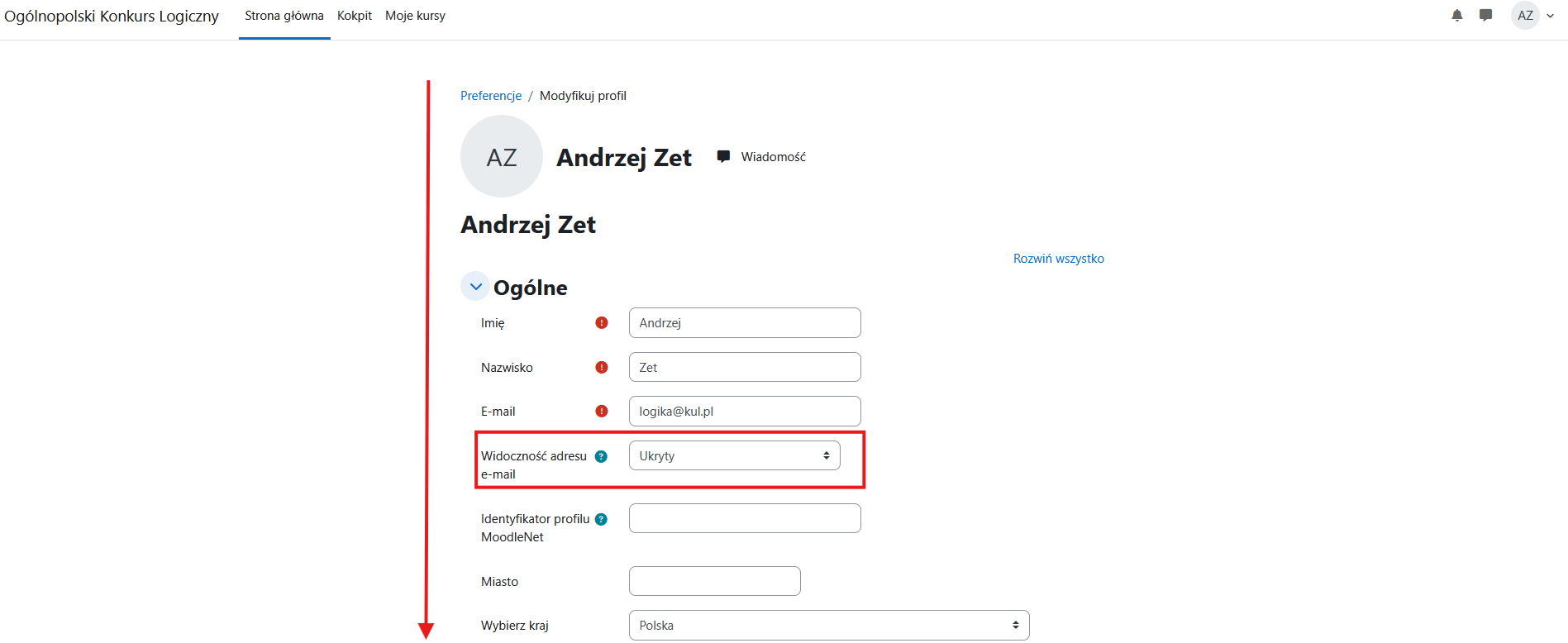
Na dole strony, w sekcji „Inne pola” wpisz REGON (9 cyfr) oraz nazwę Twojej szkoły, wskaż klasę i napisz nazwę miejscowości, w której znajduje się Twoja szkoła.
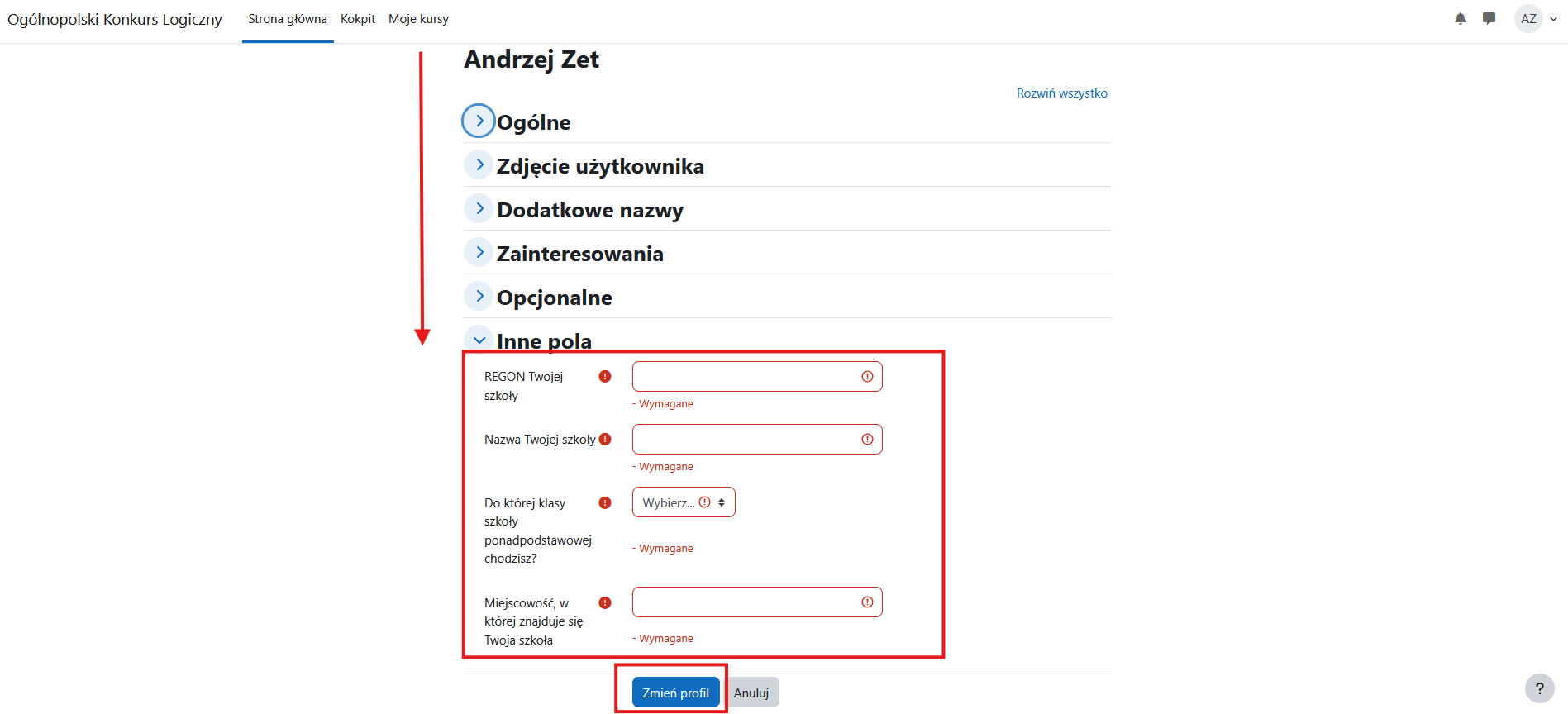
Numer REGON Twojej szkoły znajdziesz na stronie https://rspo.gov.pl/.
 Zapisz wprowadzone dane.
Zapisz wprowadzone dane.
Dziękujemy!
XIII Ogólnopolski Konkurs Logiczny – TEST PRÓBNY
Materiały przygotowujace do etapu szkolnego

lut 1, 2025 | 2024, 2025, Myślenie krytyczne
Sherlock Holmes był nie tylko świetnym praktykiem, ale także chętnie zajmował się teorią pracy detektywistycznej. Kilkukrotnie wyraźnie formułował zasady, według których – jak sądził – powinno się rozumować. Jedna z takich zasad spotkała się z dość krytycznym przyjęciem.
Zapytajcie Google’a o najbardziej znane cytaty z opowiadań o Holmesie, a na każdej chyba liście, jaką otrzymacie w odpowiedzi, znajdziecie tę oto wypowiedź Sherlocka:
kiedy wyeliminujesz wszystko, co jest niemożliwe, to, co pozostanie, nawet jeżeli jest mało prawdopodobne, musi być prawdą.
Fragment pochodzi z powieści Znak czterech, ale podobnie brzmiącą maksymę Conan Doyle wkładał w usta Sherlocka wielokrotnie także w innych, późniejszych utworach, jak choćby w opowiadaniach Diadem z berylami, Plany Bruce-Partington czy Żołnierz o bladym obliczu. Taka popularność nie może być przypadkowa. Sentencja wyraża ważną zasadę, którą dla wygody będę nazywał regułą Holmesa. Przyjrzyjmy się jej bliżej.
Reguła Holmesa
Przytoczone słowa pojawiają się w szóstym rozdziale Znaku czterech. Sherlock oraz Watson siłą wdzierają się do zaryglowanego od wewnątrz pokoju, w którym znajdują ciało zamordowanego mężczyzny. Przyjaciel Holmesa próbuje zrozumieć, jakim cudem zabójca dostał się do pomieszczenia. Detektyw formułuje omawianą regułę, po czym ciągnie swój wywód:
Wiemy, że nie wszedł przez drzwi, okno lub komin. Wiemy także, że nie mógł być ukryty w pokoju, ponieważ tu nie ma gdzie się ukryć. Którędy w takim razie się dostał?
– Wszedł przez dziurę w dachu! […]
– Oczywiście! Musiał tak właśnie zrobić.
Dżentelmeni eliminują jako nieprawdziwe wszystkie możliwe opcje poza jedną, która siłą rzeczy musi być prawdziwa.
Schemat tego rozumowania – rozumowania według reguły Holmesa – proponuję przedstawić następująco:
Schemat reguły Holmesa
Przesłanka 1: A1 lub A2 lub … lub An.
Przesłanka 2: Nieprawda, że A2 i nieprawda, że A3 i … i nieprawda, że An.
Wniosek: A1.
W tym miejscu może ktoś zaprotestować. Przecież Holmes mówi o niemożliwościach i prawdopodobieństwach, a w sugerowanej rekonstrukcji schematu brak tych pojęć. Choć w ogóle włączenie ich do rozważań mogłoby się okazać owocne, w felietonie tym zdecydowałem się je pominąć. Pominięcie jest, jak sądzę, zgodne z duchem tekstu Conan Doyla, za czym przemawia chociażby przytoczony przykład. Bohaterowie stwierdzają, że morderca nie wszedł do pokoju ani przez drzwi, ani przez okno, ani przez komin. Nie stwierdzają, że było niemożliwe, aby wszedł którąś z tych dróg. Odrzucają pewne opcje jako po prostu fałszywe, a nie jako niemożliwe. Ponadto brak powodów, aby ostatni, niewyeliminowany wariant, czyli wejście przez dziurę w dachu, traktować jako szczególnie mało prawdopodobny, zwłaszcza w porównaniu z wykluczonym wejściem przez komin. Wzmianki o niemożliwości i małym prawdopodobieństwie należy potraktować raczej jako zabiegi retoryczne niż istotne komponenty samej zasady. Dodatkowo świadczy o tym jeszcze jeden fakt. W rozdziale pierwszym tej samej powieści Holmes podaje inne, nieco rzadziej cytowane sformułowanie dyskutowanej reguły:
Po wyeliminowaniu wszystkich pozostałych faktów pozostaje wyłącznie jedna możliwość, która na pewno jest prawdziwa.
Tutaj brak już jakichkolwiek wtrętów o niemożliwościach i prawdopodobieństwach. Stąd ostatecznie taki a nie inny kształt zaproponowanego schematu.
Reguła Holmesa a wnioskowanie do najlepszego wyjaśnienia
Schemat reguły Holmesa może się wydać podobny od omawianego poprzednim razem schematu wnioskowania do najlepszego wyjaśnienia (zwanego też wnioskowaniem abdukcyjnym). W obu przypadkach z jakiejś gamy dostępnych opcji wybiera się jedną. Mimo to schematy różnią się dość istotnie i to co najmniej z dwóch powodów.
Po pierwsze, aby alternatywa tworząca pierwszą przesłankę reguły Holmesa okazała się prawdziwa musi ona zawierać wszystkie możliwe opcje. Natomiast wymienione w schemacie wnioskowania abdukcyjnego możliwe wyjaśnienia nie muszą – i w praktyce rzadką są – wszystkimi możliwymi wyjaśnieniami. Rozważa się raczej tylko te w miarę rozsądne. Po drugie, zgodnie z regułą Holmesa do wniosku dochodzi się w sposób negatywny, tzn. eliminując jako nieprawdziwe wszystkie opcje z wyjątkiem jednej. Z kolei w przypadku abdukcji postępowanie jest raczej pozytywne. Skupiamy się na zaletach dostępnych opcji i wybieramy tę najlepszą, zamiast wykazywać fałszywość pozostałych.
Jak pisałem poprzednio, wszystko to sprawia, że rozumowanie abdukcyjne jest rozumowaniem uprawdopodobniającym, nie zaś dedukcyjnym. Nawet najlepsze wyjaśnienie jakiegoś faktu z puli iluś tam rozważanych możliwych wyjaśnień zawsze może się okazać fałszywe. A jak jest w przypadku rozumowań przebiegających według reguły Holmesa?
Czy reguła Holmesa jest regułą dedukcyjną?
Łatwo dostrzeżecie chyba, Czytelnicy, że reguła Holmesa jest regułą dedukcyjną. Jeśli alternatywa kilku zdań jest prawdziwa, a wszystkie jej człony z wyjątkiem jednego są fałszywe, to ten ostatni człon alternatywy musi okazać się prawdziwy. Mówiąc prościej, jeśli znamy wszystkie możliwe warianty jakiejś sytuacji i wiemy, że wszystkie z wyjątkiem jednego nie zachodzą, to możemy być pewni, że ten ostatni zachodzi. Prawdziwość przesłanek gwarantuje prawdziwość wniosku.
O dedukcyjnym charakterze reguły Holmesa można się także przekonać w jeszcze inny sposób. Jeśli ilość dostępnych opcji ograniczona będzie do dwóch (czyli n=2), wówczas reguła Holmesa przybierze następujący kształt:
Przesłanka 1: A1 lub A2.
Przesłanka 2: Nieprawda, że A2.
Wniosek: A1.
Powyższy schemat przedstawia regułę znaną jako modus tollendo ponens (łac. tryb przez przeczenie twierdzący). Jest to jedna z podstawowych reguł dedukcyjnych. Jak widać jest też szczególnym przypadkiem reguły Holmesa. Tę ostatnią możemy wobec tego uznać po prostu za uogólnienie modus tollendo ponens.
Co jest nie tak z regułą Holmesa?
Okazuje się zatem, że przynajmniej czasami Sherlock rozumuje jednak w sposób dedukcyjny. Wnioskowania przebiegające według reguły Holmesa nie są tymi najbardziej charakterystycznymi dla legendarnego detektywa, tymi, którym poświęcone były dwa poprzednie felietony, ale mimo wszystko są przez niego przeprowadzane.
Fakt, że jakieś rozumowanie przebiega według schematu dedukcyjnego, nie jest wszelako wystarczającym powodem, aby uznać wniosek tego rozumowania za prawdziwy. Może się zdarzyć, że wśród przesłanek rozumowania znajdą się zdania fałszywe. W takim przypadku mówimy o błędzie materialnym, a rozumowanie zawierające przynajmniej jedną fałszywą przesłankę nazywamy niepoprawnym materialnie. Wnioskowi takiego rozumowania nie można oczywiście ufać. Jeśli wychodzimy od fałszywych informacji, to nawet jeśli struktura wnioskowania jest dedukcyjnie poprawna, wniosek może się okazać fałszywy. Może, ale – uwaga – nie musi. Wnioski niektórych rozumowań niepoprawnych materialnie są prawdziwe. Dzieje się tak niejako przypadkiem, niezależnie od przesłanek, jednakże sytuacji takich nie można wykluczyć. To zresztą stanowi źródło problemu. Rozumowania niepoprawne materialnie są bezużyteczne nie dlatego, że ich wnioski są zawsze fałszywe (wiedza, że jakieś zdanie jest fałszywe to zawsze jest już jakaś wiedza), ale właśnie dlatego, że w ich przypadku nigdy nie wiadomo, czy wniosek jest prawdziwy czy fałszywy. Błąd materialny w równej mierze może dotyczyć rozumowań dedukcyjnych, jak i uprawdopodobniających.
Dla zobrazowania opisanych zależności weźmy wzmiankowane wnioskowanie Holmesa i Watsona. Ustaliliśmy, że jest ono dedukcyjne. Jeśli zatem jest dodatkowo poprawne materialnie, czyli jeśli wszystkie jego przesłanki są prawdziwe, to i wniosek jest prawdziwy. Rzeczywiście jeśli wymienione przez Holmesa sposoby dostania się mordercy do pomieszczenia są wszystkimi możliwymi i jeśli poza dziurą w dachu zabójca nie skorzystał z żadnej z nich, to niewątpliwie zabójca wszedł do pomieszczenia właśnie przez tę dziurę. Jeśli jednak okazałoby się, że są jeszcze jakieś inne drogi prowadzące do pokoju (przykładowo tajemne wejście ukryte za regałem) lub gdyby okazało się, że któraś z wyeliminowanych możliwości została odrzucona zbyt pochopnie, wówczas nie można już być pewnym, że zabójca wszedł przez dziurę. Ale nawet wówczas opcji tej nie można wykluczyć i mimo wszystko może się ona okazać prawdziwa.
W przypadku niektórych rozumowań niepoprawnych materialnie fałszywość przesłanki lub przesłanek jest zręcznie ukrywana i może być łatwo przeoczona przez odbiorcę. Pojawiają się głosy – choć przyznać muszę, że raczej w tekstach popularnych niż akademickich – jakoby z regułą Holmesa wiązało się takie właśnie niebezpieczeństwo. Ten szczególny rodzaj defektu otrzymał nawet nazwę „błędu Sherlocka Holmesa” (The Sherlock Holmes Fallacy; Holmesian Fallacy). Najczęściej polega on na przeoczeniu fałszywości pierwszej przesłanki schematu reguły Holmesa. Rozumujący akceptuje alternatywę kilku wariantów jako zupełną, tzn. wyczerpującą wszystkie możliwe opcje, podczas gdy faktycznie niektóre możliwości zostają pominięte. (Na marginesie dodam, że błąd Holmesa jest podobny do błędu fałszywej alternatywy. Być może nawet jest po prostu jego szczególnym przypadkiem. Więcej o tym ostatnim błędzie możecie przeczytać na łamach „Filozofuj!” w tym miejscu)
W praktyce bardzo trudno jest uwzględnić wszystkie możliwe scenariusze. Nawet Holmesowi, którego zdolność obserwacji dorównywała jego zdolności wnioskowania, zdarzało się przeoczyć niektóre opcje (powyżej wskazałem ukryte za regałem tajemne przejście jako przykład takiego przeoczonego wariantu). Dlatego gdy usłyszycie buńczuczne zapewnienia, że spośród wszystkich możliwości tylko jedna wchodzi w rachubę, krytycznie i spokojnie rozważcie, czy rzeczywiście uwzględniono wszystkie warianty.

lut 1, 2025 | 2024, 2025, Myślenie krytyczne
Sherlock Holmes niejednokrotnie nazywa przeprowadzane przez siebie wnioskowania dedukcjami. Jeśli dedukcję rozumie się w sposób potoczny, to z deklaracją tą nie ma problemu. Jeśli natomiast rozumieć dedukcję w ściśle technicznym sensie, to typowe rozumowania Holmesa należy uznać raczej za wnioskowania uprawdopodobniające niż dedukcyjne. Taka była konkluzja poprzedniego felietonu. Rozumowań uprawdopodobniających jest jednak wiele rodzajów. Są uogólnienia indukcyjne, wnioskowania do autorytetu, wnioskowania przez analogię, wnioskowania statystyczne i wiele innych. Który z tych rodzajów jest charakterystyczny dla Holmesa?
Aby odpowiedzieć na powyższe pytanie, przyjrzyjmy się tym typowym dla Holmesa rozumowaniom. O przykłady nie będzie trudno, gdyż znaleźć je można w niemal każdym opowiadaniu o przygodach genialnego detektywa. Poprzednim razem jako ilustrację podałem wnioskowanie z początku pierwszego opowiadania, czyli ze Skandalu w Bohemii. Teraz dla odmiany proponuję sięgnąć do tekstu zatytułowanego Żółta twarz.
Dwa przykłady
Sherlock wraz z doktorem Watsonem wracają na Baker Street z wiosennej przechadzki. W domu dowiadują się, że podczas ich nieobecności detektywa odwiedził klient. Zdenerwowany jegomość, nie mogąc wytrzymać przedłużającego się oczekiwania, wyszedł na spacer. W roztargnieniu pozostawił jednak w mieszkaniu bohaterów fajkę. Na jej podstawie Holmes wyciąga wiele wniosków na temat właściciela. M.in. przedstawia Watsonowi następujące rozumowanie:
Zauważ, że zwęglenie występuje po prawej stronie. Stąd wniosek, że właściciel jest mańkutem. Przyłóż fajkę do ognia, a przekonasz się, że podstawiłeś jej lewą stronę. Bo nie jesteś mańkutem. Mógłbyś czasem zrobić inaczej, ale nie stale. Tę zawsze przypalano z prawej strony.
Pomijając pewne szczegóły, wnioskowanie powyższe, a przynajmniej jego wyraźnie wyartykułowane składniki, najprościej zrekonstruować mniej więcej tak:
Wnioskowanie 1)
Przesłanka: Fajka jest zwęglona z prawej strony.
Wniosek: Właściciel fajki jest leworęczny.
Oto typowe rozumowanie Holmesa. Oczywiście nie jest ono dedukcyjne w sensie ścisłym, gdyż wniosek nie wynika logicznie z przesłanki. Można sobie wyobrazić, że czyjaś fajka jest zwęglona z prawej strony, mimo że ten ktoś nie jest leworęczny. Przykładowo może ktoś praworęczny chcieć uchodzić za leworęcznego i dlatego celowo przypalać fajkę z prawej strony, albo może pożyczyć fajkę swojemu leworęcznemu przyjacielowi, który przypalił ją z prawej strony, albo może założyć się z kimś o to, że nie tylko leworęczni przypalają fajkę z prawej strony i jako praworęczny próbować to wykazać, albo… Spośród tych i innych możliwości zaproponowane przez Sherlocka wyjaśnienie faktu, że fajka przypalona jest z prawej strony wydaje się najbardziej rozsądne.
Pozostałe rozumowania sprowokowane wspomnianą fajką są podobne. Wszystkie one okazują się jednak tylko zabawą, wprawką do właściwej roboty detektywistycznej. Rozkojarzony właściciel fajki – niejaki Grant Munro – wraca i przedstawia sprawę, która dotyczy jego żony Effie. (Ostrzegam, że od teraz pojawi się wiele spojlerów.) Munro wyznaje, że pomimo jej młodego wieku poznał Effie już jako wdowę. Pierwszego męża poznała w Ameryce, a po jego śmierci wróciła do Wielkiej Brytanii. Klient zapewnia, że od trzech lat prowadzą szczęśliwe życie małżeńskie. Niestety ostatnio Effie zaczęła się zachowywać w niezrozumiały i niepokojący sposób. W tajemniczych okolicznościach wydała niebagatelną sumę 100 funtów, a co gorsza w sekrecie odwiedza sąsiedni dom, do którego właśnie wprowadzili się nowi lokatorzy. Wśród lokatorów jest zagadkowa postać o tytułowej żółtej twarzy. Kiedy zdenerwowany Munro postanawia przemocą poznać tożsamość nowych sąsiadów, ci znikają. Holmes każe klientowi wracać do domu, a w razie powrotu sąsiadów – zadepeszować. W takim przypadku on wraz w Watsonem niezwłocznie przybędą na miejsce.
Po wyjściu klienta Holmes przedstawia Watsonowi swoją teorię. Osobliwe zachowanie Effie tłumaczy szantażem. Uważa, że tajemnicza postać o żółtej twarzy to jej pierwszy mąż, od którego – z takiego lub innego powodu – musiała uciec. Skłamała na temat jego śmierci, a teraz zmuszana jest do kupowania jego milczenia wysokimi kwotami.
Znów upraszczając znacznie, wnioskowanie Holmesa można zrekonstruować tak:
Wnioskowanie 2)
Przesłanka: Effie zachowuje się osobliwie (wydaje duże kwoty na niewiadome cele, w tajemnicy odwiedza nieznajomych z sąsiedniego domu).
Wniosek: Effie jest szantażowana przez jej byłego męża.
Choć sytuacja jest tu dużo bardziej skomplikowana niż w przypadku wnioskowania 1), to zasadniczy typ wnioskowania pozostaje ten sam. Zaproponowany przez Holmesa wniosek wydaje się trafnym wyjaśnieniem opisanych w przesłance faktów. O tym, że rozumowanie to nie jest niezawodne, najlepiej przekonać się, czytając opowiadanie Conana Doyle’a do końca. Zawiera ono rzadki przykład pomyłki Holmesa, a prawdziwe wyjaśnienie zachowania Effie jest zgoła odmienne. Mimo że w tym konkretnym wypadku rozumowanie Holmesa zawiodło, to wnioskowania tego typu są wysoko cenionymi i powszechnie stosowanymi rozumowaniami uprawdopodobniającymi. Nazywa się je niekiedy wnioskowaniami abdukcyjnymi.
Wnioskowanie do najlepszego wyjaśnienia
Termin „abdukcja” nie jest jednoznaczny. Do języka logiki wprowadził go amerykański filozof Charles Sanders Peirce. Nie wypracował on jednak jednolitej i spójnej koncepcji abdukcji. Poza tym rozumiał ją nieco inaczej, niż rozumie się ją dzisiaj. Być może dlatego współcześnie odchodzi się od nazwy „abdukcja” i zastępuje się ją raczej określeniem „wnioskowanie do najlepszego wyjaśnienia”. W niniejszym felietonie zajmuję się wyłącznie abdukcją jako wnioskowaniem do najlepszego wyjaśnienia i obu terminów używam zamiennie.
Ogólna struktura tego wnioskowania jest następująca. Przesłanka lub przesłanki zawierają zwykle opis jakiegoś stanu rzeczy. Istnieje ileś konkurencyjnych hipotez, z których każda wyjaśnia, jak doszło do zajścia opisanego w przesłankach stanu rzeczy. Zgodnie z naczelną regułą wnioskowania do najlepszego wyjaśnienia (wyrażoną expressis verbis w samej jego nazwie) jako wniosek należy przyjąć najlepszą z rozważanych hipotez.
Schematycznie można to przedstawić tak:
Schemat wnioskowania do najlepszego wyjaśnienia
Przesłanka 1: Zaszedł stan rzeczy S.
Przesłanka 2: W1, W2, … Wn są wyjaśnieniami stanu rzeczy S.
Przesłanka 3: Najlepsze spośród wyjaśnień W1, W2, … Wn. jest Wj.
Wniosek: Prawdziwe jest Wj.
Z wnioskowaniem do najlepszego wyjaśnienia wiąże się wiele dyskutowanych współcześnie kwestii. Jedna z głównych dotyczy oczywiście tego, jak rozpoznać, które wyjaśnienie jest najlepsze. Rozważane są różne kryteria. Wśród propozycji znaleźć można prostotę (im prostsza hipoteza, tym lepsza), zasięg (lepsza jest ta, która wyjaśnia więcej) lub zachowawczość (wyżej oceniane są te, które zgadzają się z powszechnie akceptowanymi i dobrze uzasadnionymi twierdzeniami w danej dziedzinie). Brak natomiast ostatecznych rozstrzygnięć.
Mimo to omawiane wnioskowania są bardzo powszechne i to nie tylko w praktyce fikcyjnych lub rzeczywistych detektywów. Uzasadnienie wielu teorii naukowych podaje się właśnie w formie abdukcyjnej, próbując wykazać, że teorie te najlepiej tłumaczą obserwowane zjawiska. W życiu codziennym również często rozumujemy w taki sposób. Widzicie w kuchni rozlane na stole mleko i od razu zgadujecie, że odpowiedzialne jest za to wasze kilkuletnie dziecko. Samochód staje wam nagle w polu i natychmiast uświadamiacie sobie, że dawno nie był tankowany. Inne przykłady bez trudu znajdziecie sami.
Niekiedy zamiast podawać kilka konkurencyjnych hipotez, od razu wskazuje się tę, którą uznaje się za najlepszą. Tak było zarówno w podanych przed chwilą przykładach, jak i w opisanych wcześniej rozumowaniach Holmesa. Niemniej wciąż najlepiej interpretować rozumowania takie jako wnioskowania do najlepszego wyjaśnienia. Gdyby trzeba było, te inne gorsze hipotezy zawsze można podać.
Wnioskowanie redukcyjne
O abdukcji i wnioskowaniach do najlepszego wyjaśnienia przeczytać można głównie w literaturze anglojęzycznej. W tekstach polskich wspomniane terminy pojawiają się rzadko, a w nieco starszych klasycznych podręcznikach nie ma ich wcale. W rodzimych publikacjach pojawiają się za to tzw. wnioskowania redukcyjne, które przypominają omawiane rozumowania abdukcyjne.
Wnioskowania redukcyjne określa się zwykle tak. Wniosek takiego rozumowania nie wynika logicznie z przesłanek, ale z wniosku oraz pewnej przesłanki (często niewyrażonej wprost) wynika inna przesłanka. Innymi słowy, wnioskowanie redukcyjne można przekształcić we wnioskowanie dedukcyjne przez zamianę miejscami wniosku i jednej z przesłanek. Odnośnie do wnioskowania 1) można by w kluczu tym powiedzieć, że fakt leworęczności właściciela fajki (wniosek) nie wynika z tego, że fajka jest przypalona z prawej strony (przesłanka), ale z tego, że właściciel jest leworęczny (wniosek), w połączeniu z ukrytą przesłanką warunkową (Jeśli właściciel fajki jest leworęczny, to fajka jest zwęglona z prawej strony) wynika logicznie, że fajka jest zwęglona z prawej strony (przesłanka). Wnioskowanie 1) można zatem przerobić na takie wnioskowanie dedukcyjne:
Wnioskowanie 1A)
Przesłanka 1 (ukryta): Jeśli właściciel fajki jest leworęczny, to fajka jest zwęglona z prawej strony.
Przesłanka 2 (oryginalny wniosek): Właściciel fajki jest leworęczny.
Wniosek (oryginalna przesłanka): Fajka jest zwęglona z prawej strony.
Do wnioskowania 1A) można mieć zastrzeżenia. Można przykładowo wątpić w prawdziwość pierwszej przesłanki. Jeśli mimo wszystko zaakceptujemy ją i uznamy, iż jest ona ukrytą przesłanką wnioskowania 1), to tym samym uznamy wnioskowanie 1) za redukcyjne.
W ogólności jednak rozumowań abdukcyjnych nie należy utożsamiać z redukcyjnymi. Nawet bowiem jeśli niekiedy z wniosku rozumowania abdukcyjnego wynika jedna z jego przesłanek, to z pewnością nie jest tak zawsze. Aby się o tym przekonać, wystarczy wrócić do wnioskowania 2), w przypadku którego przesłanka nie wynika z wniosku. Oczywiście mógłby ktoś zaproponować taką modyfikację:
Wnioskowanie 2A)
Przesłanka 1 (ukryta): Jeśli Effie jest szantażowana przez jej byłego męża, to Effie zachowuje się osobliwie (wydaje duże kwoty na niewiadome cele, w tajemnicy odwiedza nieznajomych z sąsiedniego domu).
Przesłanka 2 (oryginalny wniosek): Effie jest szantażowana przez jej byłego męża.
Wniosek (oryginalna przesłanka): Effie zachowuje się osobliwie (wydaje duże kwoty na niewiadome cele, w tajemnicy odwiedza nieznajomych z sąsiedniego domu).
Jednakże w tym wypadku pierwszej przesłanki nie sposób już zaakceptować. Można się zgodzić, że szantaż zwiększyłby prawdopodobieństwo dziwnego zachowania Effie, ale nierozsądne byłoby twierdzić, że na pewno spowoduje on dziwne zachowanie Effie.
Kwestia relacji między wnioskowaniami abdukcyjnymi i redukcyjnymi nie jest oczywista i domaga się obszerniejszego komentarza, na który tutaj nie ma miejsca. W każdym razie ważne, aby zapamiętać, że nie należy redukować wnioskowań abdukcyjnych do wnioskowań redukcyjnych.

lut 1, 2025 | 2024, 2025, Myślenie krytyczne
Sherlock Holmes jest jedną z tych postaci fikcyjnych, które goszczą nie tylko na kartach dzieł literackich, ale także podręczników do logiki i wprowadzeń do krytycznego myślenia. Opowiadania opisujące rozwikłane przez genialnego detektywa zagadki kryminalne dostarczają wielu przykładów wdzięcznych do analizy wnioskowań. Jednocześnie Holmes jest często oskarżany przez autorów wspomnianych podręczników o poważny błąd. Zarzuca mu się, że niewłaściwie identyfikuje rodzaj swoich charakterystycznych rozumowań. Czy zarzut ten jest słuszny?
Na początku były dwie powieści. Później pojawiły się opowiadania publikowane co miesiąc w The Strand Magazine. To głównie te ostatnie rozsławiły Sherlocka Holmesa. Pierwsze z tych opowiadań – Skandal w Bohemii – zaczyna się od wizyty doktora Johna Watsona na Baker Street 221B. Przyjaciel i biograf Holmesa oraz jego niegdysiejszy współlokator odwiedza Sherlocka po dłuższej przerwie. Mimo rozłąki detektyw zdaje się znać aktualną sytuację przyjaciela, jak gdyby rozmawiał z nim wczoraj. Zdziwionemu Watsonowi tak tłumaczy pochodzenie posiadanych informacji:
– Skąd wiem? Widzę i dedukuję. Zauważyłem, że ostatnio bardzo zmokłeś i że masz niedbałą i niestaranną służącą. […) oczy mówią mi, że na wewnętrznej stronie lewego buta, w miejscu, gdzie odbija się światło ognia, skóra jest uszkodzona sześcioma prawie równoległymi nacięciami. Oczywiście zostało to spowodowane przez kogoś, kto bardzo niestarannie szorował krawędzie podeszwy, aby usunąć z niej zaschnięte błoto. Stąd, jak sam rozumiesz, wynika moja podwójna dedukcja, że byłeś na dworze w czasie obrzydliwej pogody, a twoja służąca jest szczególnie marnego gatunku, gdyż niszczy ci buty.
Rozumowanie powyższe proponuję zrekonstruować jako ciąg dwóch prostych wnioskowań, połączonych w ten sposób, że wniosek pierwszego z nich staje się przesłanką drugiego.
Wnioskowanie 1A)
Przesłanka: Watson ma buta uszkodzonego sześcioma równoległymi nacięciami.
Wniosek: Ktoś niestarannie czyścił niedawno buty Watsona z zaschniętego błota.
Wnioskowanie 1B)
Przesłanka: Ktoś niestarannie czyścił niedawno buty Watsona z zaschniętego błota.
Wniosek: Watson przebywał niedawno na dworze w czasie obrzydliwej pogody i ma niedbałą służącą.
Tego typu rozumowania są znakiem rozpoznawczym śledczej metody Holmesa. Opowiadania o jego przygodach są ich pełne. W cytowanym fragmencie on sam nazywa je – i to dwukrotnie – dedukcjami. Czy ma rację?
Dedukcje – wnioskowania niezawodne
Wnioskowanie rozumiane jest często – choć nie jest to jedyna opcja – jako proces myślowy polegający na przechodzeniu od pewnych zdań – zwanych przesłankami –, do innych zdań – zwanych wnioskami. Na ogół przesłanki są już akceptowane przez wnioskującego i właśnie w efekcie wnioskowania uznaje on także wniosek. W przytoczonym fragmencie Holmes podaje przykład takiego procesu myślowego.
Wszystkie wnioskowania dzieli się dychotomicznie na dedukcyjne i niededukcyjne. Podręczniki logiki wnioskowania dedukcyjne definiują zwykle jako takie, których wniosek wynika z przesłanek logicznie. Pojęcie „wynikania logicznego” jest pojęciem technicznym definiowanym często przy pomocy kolejnych pojęć technicznych (takich jak „tautologia” lub „prawo logiki”). Wszystko to jest bardzo precyzyjne i każdy, kto chce poważnie zająć się studiowaniem logiki, musi sobie cały ten warsztat terminologiczny przyswoić. Tutaj mogę natomiast posłużyć się definicją być może nieco mniej formalną, ale za to lepiej wyrażającą główne intuicje. Otóż wnioskowanie dedukcyjne to wnioskowanie niezawodne, czyli takie, w przypadku którego prawdziwość przesłanek gwarantuje prawdziwość wniosku. Znaczy to, że nie jest możliwe, aby przesłanki wnioskowania dedukcyjnego były prawdziwe, a jednocześnie jego wniosek fałszywy.
Weźmy prosty przykład dedukcji.
Wnioskowanie 2)
Przesłanka 1: Każdy przyjaciel Sherlocka Holmesa jest Brytyjczykiem.
Przesłanka 2: Watson jest przyjacielem Sherlocka Holmesa.
Wniosek: Watson jest Brytyjczykiem.
Jest oczywiste, że nie może się zdarzyć, aby przesłanki tego rozumowania były prawdziwe, a wniosek fałszywy. Jeżeli okazałoby się, że Watson nie jest Brytyjczykiem, to albo musiałoby się okazać, że nie jest przyjacielem Holmesa, albo musiałoby się okazać, że nie wszyscy przyjaciele Holmesa są Brytyjczykami, albo jedno i drugie zarazem. Prawdziwość przesłanek wnioskowania 2) rzeczywiście gwarantuje prawdziwość jego wniosku.
Wnioskowania uprawdopodobniające
Wnioskowania dedukcyjne są bardzo silnymi wnioskowaniami, właściwie najsilniejszymi. Oczywiście nie we wszystkich wnioskowaniach przesłanki wspierają wniosek aż tak mocno. Weźmy taki przykład.
Wnioskowanie 3)
Przesłanka 1: Zdecydowana większość przyjaciół Sherlocka Holmesa jest Brytyjczykami.
Przesłanka 2: Watson jest przyjacielem Sherlocka Holmesa.
Wniosek: Watson jest Brytyjczykiem.
Wniosek tego rozumowania może okazać się fałszywy, nawet jeśli jego przesłanki będą prawdziwe. Choćby zdecydowana większość przyjaciół Holmesa była Brytyjczykami, a Watson był jednym z jego przyjaciół, zawsze może się okazać, że Watson należy do mniejszości i Brytyjczykiem nie jest. Prawdziwość przesłanek nie gwarantuje w tym przypadku prawdziwości wniosku.
Mimo że wnioskowanie 3) nie jest dedukcyjne, nie jest też zupełnie bezwartościowe. Jeśli o przyjaciołach Holmesa wiedzielibyśmy tylko, że zdecydowana ich większość jest Brytyjczykami, a o Watsonie tylko, że jest przyjacielem Holmesa, to mielibyśmy pewne powody, aby sądzić, że jest on Brytyjczykiem. Nie byłyby to racje rozstrzygające kwestię w sposób pewny, ale wciąż byłby to jakieś racje. W świetle przesłanek brytyjska narodowość Watsona nie jest pewna, ale bardziej prawdopodobna niż jakakolwiek inna. Przesłanki w jakimś stopniu wspierają wniosek. Wnioskowania, w przypadku których prawdziwość przesłanek nie gwarantuje prawdziwości wniosku, ale jednak czyni ten wniosek – w mniejszym lub większym stopniu – prawdopodobnym, nazywamy wnioskowaniami uprawdopodobniającymi. W ich przypadku zawsze jest możliwe, że przesłanki okażą się prawdziwe, a jednocześnie wniosek fałszywy, ale sytuacja taka będzie mało prawdopodobna.
Rozróżnienie dedukcyjne uprawdopodobniające opisać można jeszcze w inny sposób. Wniosek rozumowania dedukcyjnego należy uznawać dokładnie w tym samym stopniu, w jakim uznaje się jego przesłanki. W przypadku wnioskowania uprawdopodobniającego wniosek należy zawsze uznawać w stopniu mniejszym aniżeli stopień, z jakim uznaje się przesłanki. Jeśli ktoś uznaje, że wszyscy przyjaciele Holmesa są Brytyjczykami, a Watson jest jednym z tych przyjaciół, to powinien z tą samą siłą uznać, że Watson jest Brytyjczykiem. Jeśli zaś ktoś uznaje, że zdecydowana większość przyjaciół Holmesa jest Brytyjczykami oraz że Watson jest przyjacielem Holmesa, to przekonanie o brytyjskiej narodowości Watsona powinien uznać za mniej pewne niż te dwa. Mówiąc obrazowo wnioskowanie dedukcyjne jest bezstratne. Przechodząc do wniosku, nie powinno się tracić nic z pewności pokładanej w przesłankach. Wnioskowanie uprawdopodobniające jest z kolei stratne, gdyż część pewności powinna być po drodze porzucona.
Wnioskowania bezwartościowe
Dla zupełności opisu dodać należy, że nie wszystkie wnioskowania niededukcyjne są wnioskowaniami uprawdopodobniającymi. Są jeszcze wnioskowania bezwartościowe, a więc takie, w przypadku których prawdziwość przesłanek nie tylko nie gwarantuje prawdziwości wniosku, ale nawet nie czyni tego wniosku prawdopodobnym, a niekiedy wręcz gwarantuje jego fałszywość. Są to po prostu rozumowania zupełnie wadliwe, a zatem bezużyteczne, a nawet szkodliwe. Oto przykład.
Wnioskowanie 4)
Przesłanka 1: Zdecydowana większość przyjaciół Sherlocka Holmesa jest Brytyjczykami.
Przesłanka 2: Watson jest przyjacielem Sherlocka Holmesa.
Wniosek: Watson jest Włochem.
Ostatecznie wszystkie wnioskowania dzielimy na dedukcyjne i niededukcyjne, te ostatnie dzieląc dalej na uprawdopodobniające i bezwartościowe.
Bałagan terminologiczny
W tym miejscu muszę Cię, Czytelniku, ostrzec. Przedstawione powyżej wyjaśnienia i podziały są dość standardowe, ale z omawianymi kwestiami wiąże się spore zamieszanie terminologiczne. Po pierwsze, termin „dedukcja” bywa przez różnych autorów definiowany nieco odmiennie. Są to różnice subtelne, na których opisanie nie ma tutaj miejsca, ale o których lojalnie informuję.
Po drugie, brak jest powszechnej zgody co do tego, jak określać wnioskowania niededukcyjne. Niekiedy nazywa się je wnioskowaniami zawodnymi (jako przeciwieństwo wnioskowań niezawodnych, czyli dedukcyjnych). To nie wszystkim się podoba, gdyż zdaje się sugerować, że wnioskowania te zawodzą co do zasady, a przecież tak nie jest. Dlatego zamiast zawodnymi nieporadnie nazywa się je niekiedy nie-niezawodnymi. W piśmiennictwie anglojęzycznym z kolei, które coraz silniej oddziałuje także na nazewnictwo polskie, rozumowania dedukcyjne przeciwstawia się często indukcyjnym. Przy takim postawieniu sprawy trzeba pamiętać, iż słowo „indukcja” staje się terminem wieloznacznym. W sensie szerokim oznacza wówczas wszystkie wnioskowania niededukcyjne, w sensie wąskim – pewien szczególny rodzaj wnioskowania niededukcyjnego.
I jeszcze jedna uwaga. Powyżej używam słów „wnioskowanie” i „rozumowanie”. Chociaż można znaleźć próby mniej lub bardziej radykalnego odróżniania jednego od drugiego (przykładowo wnioskowanie traktuje się niekiedy jako szczególny przypadek rozumowania), tutaj używam tych terminów zamiennie. Pozostaje to w zgodzie z dość powszechną praktyką językową.
Jak rozumuje Holmes?
Możemy teraz powrócić do tytułowego pytania. Nie trudno zauważyć, że przytoczone na wstępie wnioskowania 1A) i 1B) nie są rozumowaniami dedukcyjnymi w podanym powyżej sensie. Myślę, że bez trudu jesteś, Czytelniku, w stanie opisać sytuację, w której przesłanka każdego z tych wnioskowań jest prawdziwa, a jednocześnie wniosek fałszywy (Watson może mieć przecież but porysowany z innego powodu niż nieuwaga jego służącej). Tym samym, nawet jeśli wyciągnięte przez Holmesa wnioski okazują się ostatecznie prawdziwe, nie znaczy to, że prawdziwość ich zagwarantowana jest przez prawdziwość przesłanek, od których wychodzi. Nawiasem mówiąc, o tym, że rozumowania Holmesa nie są niezawodne, dobitnie świadczy historia opisana w opowiadaniu Żółta twarz.
Dlaczego więc Holmes nazywa swoje rozumowania dedukcjami? Cytat, którym posłużyłem się na wstępie, pochodzi z tłumaczenia autorstwa Ewy Łozińskiej-Małkiewicz. Polskie „dedukuję” jest jej przekładem angielskiego deduce. Z niemałym zaskoczeniem odkryłem, że dawniejsi tłumacze rozstrzygali sprawę odmiennie. W wydaniu z 1955 r. Irena Doleżał-Nowicka oddaje to samo deduce jako „wyciągam odpowiednie wnioski”. W całej tej edycji zresztą, na którą składają się przekłady kilku autorów, polskie słowo „dedukuję” i jego pochodne pojawiają się jako tłumaczenie angielskiego deduce sporadycznie. Dawniejsze przekłady stają się zrozumiałe, gdy skonfrontuje się je ze słownikiem języka angielskiego. Internetowy Cambridge Dictionary definiuje „dedukować” (ang. deduce) jako „dochodzić do odpowiedzi poprzez ostrożne rozważanie znanych faktów” (ang. to reach an answer […] by carefully thinking about the known facts). Pod takie – nazwijmy je potocznym – rozumienie dedukowania procesy myślowe Holmesa z pewnością podpadają.
Mamy zatem dwie opcje. Możemy interpretować używane przez Holmesa słowo „dedukować” w ścisłym sensie logicznym i w konsekwencji uznać, że „najdoskonalej rozumująca maszyna, jaką kiedykolwiek oglądał świat” – jak określa Sherlocka Watson – popełnia dziecinny błąd, niepoprawnie identyfikując naturę własnych rozumować. Albo możemy interpretować jego „dedukowanie” w sensie potocznym, co nie będzie stawiało go w kłopotliwej sytuacji. Zasada życzliwości nakazuje opowiedzieć się za drugim rozwiązaniem. Jeśli jej posłuchamy, utyskiwania na to, że wbrew własnym deklaracjom Holmes wcale nie dedukuje, okażą się tylko przykładem błędu ekwiwokacji. O tym ostatnim zaś możesz, Czytelniku, przeczytać w poprzednim felietonie.